
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由.

 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.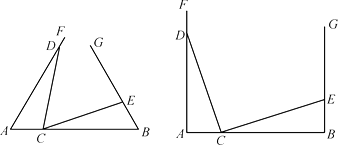
Ⅰ、如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60或∠FAB=∠GBA=90两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
Ⅱ、若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.

(1)用t的代数式表示:AE= ;DF= ;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系?若存在,证明你的结论;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC═8,tanA═ ![]() ,那么CF:DF═
,那么CF:DF═ 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣ ![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为28块时,白色瓷砖块数为( )

A. 27 B. 28 C. 33 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)-14-![]() ×[2-(-3)]; (2)(-3)-1
×[2-(-3)]; (2)(-3)-1![]() ×
×![]() -6÷|-
-6÷|-![]() |;
|;
(3)2×[5+![]() ]-(-|-4|÷
]-(-|-4|÷![]() );(4)-
);(4)-![]() -[-3+(-3)÷(-
-[-3+(-3)÷(-![]() )].
)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com