
����Ŀ������֪�߶�AB��ͬ����FAB����GBA������������AF��BG�Ϸֱ�ȡ��D��E�����߶�AB��ȡ��C������DC��EC��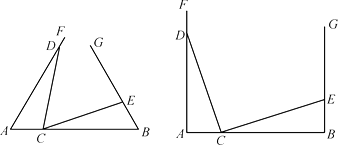
����ͼ����AD��3��BE��1����ADC�ա�BCE���ڡ�FAB����GBA��60���FAB����GBA��90�����������ѡһ�֣�����������⣺
���߶�AB�ij����Ƿ����仯��ֱ��д�����Ȼ�仯��Χ��
�ڡ�DCE�Ķ����Ƿ����仯��ֱ��д��������仯��Χ��
����AD��a��BE��b����FAB����GBA�������ҡ�ADC�͡�BCE������������ȫ�ȣ��������
���߶�AB�ij��Ȼ�ȡֵ��Χ����˵�����ɣ�
�ڡ�DCE�Ķ�����ȡֵ��Χ����˵�����ɣ�
���𰸡�ѡͼһ
��AB��4�����䣻
�ڡ�DCE��60.
��a ![]() bʱ����AB�� a��b�� �ڡ�DCE����
bʱ����AB�� a��b�� �ڡ�DCE����
��a=bʱ����AB��0. ��0����DCE��180.
ѡͼ��
�� AB��4�����䣻 �ڡ�DCE��90.
��a ![]() bʱ����AB�� a��b�� �ڡ�DCE����
bʱ����AB�� a��b�� �ڡ�DCE����
��a=bʱ���� AB��0. ��0����DCE��180.
��������ѡͼһ
�١ߡ�ADC�ա�BCE��
��BC=AD=3��AC=BE=1��
��AB=AC+BC=4��
��AB��4�����䣻
�ڡߡ�FAB����GBA��60��
���ADC+��ACD=120��
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=120��
���DCE��60.
��a ![]() bʱ�����ADC�ա�BCE��
bʱ�����ADC�ա�BCE��
�١ߡ�ADC�ա�BCE����BC=AD=a��AC=BE=b����AB�� a��b��
�ڡ�DCE����
��a=bʱ�����ADC�ա�BEC����AC=BC����
��AB��0. ��0����DCE��180.
ѡͼ��
�١ߡ�ADC�ա�BCE��
��BC=AD=3��AC=BE=1��
��AB=AC+BC=4��
��AB��4�����䣻
�ڡߡ�FAB����GBA��90��
���ADC+��ACD=90��
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=90��
���DCE��90.
��a ![]() bʱ�����ADC�ա�BCE��
bʱ�����ADC�ա�BCE��
�١ߡ�ADC�ա�BCE����BC=AD=a��AC=BE=b����AB�� a��b��
�ڡߡ�FAB����GBA������
���ADC+��ACD=180-����
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=180-����
���DCE������
��a=bʱ�����ADC�ա�BEC����AC=BC����
��AB��0. ��0����DCE��180.
���ݡ�ADC���BCE���Զ������Ӧ�ߣ�����֪��FAB����GBA������A��B��Ӧ��
�ڢ��У����ݡ�ADC�ա�BCE���õ���Ӧ����ȣ��ɵ��������õ�AB�ij������ݶ�Ӧ����ȡ��������ڽǺ���ƽ�ǵĶ������á�DCE��
�ڢ���Ҫ��D��C��Ӧ��D��E��Ӧ��������������ۣ��������������.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪����x�ķ���kx=11��2x�������⣬������k��ֵΪ�� ����
��2����a+b+c=0����a��b��c�����½��ۣ�
��a��0��c��0��
�ڹ���x�ķ���ax+b+c=0�Ľ�Ϊx=1��
��a2=��b+c��2��
��![]() ��ֵΪ0��2��
��ֵΪ0��2��
���������ϵ�A��B��C��ʾ��a��b��c����b��0�����߶�AB���߶�BC�Ĵ�С��ϵ��AB��BC��
������ȷ�Ľ������� ������д��ȷ���۵���ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ������ô�����Χ�������м��ö��ŶϿ����磺{1��2����3}��{��2��7��![]() ��19}�����dz�֮Ϊ���ϣ����е�ÿ������Ϊ�ü��ϵ�Ԫ�أ����һ������Ԫ�ؾ�Ϊ�������ļ������㣺��������a�Ǽ��ϵ�Ԫ��ʱ��2015��aҲ����������ϵ�Ԫ�أ������ļ������dz�Ϊ�õļ��ϣ����缯��{2015��0}����һ���õļ��ϣ�
��19}�����dz�֮Ϊ���ϣ����е�ÿ������Ϊ�ü��ϵ�Ԫ�أ����һ������Ԫ�ؾ�Ϊ�������ļ������㣺��������a�Ǽ��ϵ�Ԫ��ʱ��2015��aҲ����������ϵ�Ԫ�أ������ļ������dz�Ϊ�õļ��ϣ����缯��{2015��0}����һ���õļ��ϣ�
��1������{2015}_____�õļ��ϣ�����{��1��2016}_____�õļ��ϣ����վ���ǡ����ǡ�����
��2����һ���õļ���������һ��Ԫ��Ϊ4011����ü����Ƿ������С��Ԫ�أ�������ڣ���ֱ��д���𰸣�����˵�����ɣ�
��3����һ���õļ�������Ԫ��֮��Ϊ����M����22161��M��22170����ü��Ϲ��м���Ԫ�أ�˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����ƽ��ֱ������ϵ�У��ı���OBCD�������Σ���D��0,2������E���߶�OB�ӳ�����һ�㣬M���߶�OB��һ���㣨������O��B������MN��DM������ΪM������CBE��ƽ�����ڵ�N.
��1�����C�����ꣻ
��2����֤��MD=MN��
��3����ͼ��2��������DN��BC��F������FM��̽���߶�MF��CF��OM֮����ʲô������ϵ����֤����Ľ���.
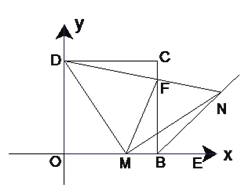
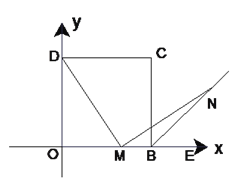
ͼ��1�� ͼ��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij�����ι㳡���ĽǶ���һ��뾶��ͬ��![]() Բ�εIJݵأ���֪Բ�εİ뾶Ϊr�ף�����������Ϊa�ף���Ϊb�ף�
Բ�εIJݵأ���֪Բ�εİ뾶Ϊr�ף�����������Ϊa�ף���Ϊb�ף�
��1������ʽ��ʾ�㳡�յص������

��2���������εij�Ϊ300�ף���Ϊ200�ף�Բ�εİ뾶Ϊ10�ף�����㳡�յص�����������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϵĶ��㣨�����B��C��D�غϣ����ҡ�EAF=45�㣬AE��AF��Խ���BD�ֱ��ཻ�ڵ�G��H,����EH��EF,�����н��ۣ��� ��ABH�ס�GAH; �� ��ABG�ס�HEG; �� AE= ![]() AH; �� EH��AF; �� EF=BE+DF
AH; �� EH��AF; �� EF=BE+DF
������ȷ���У� ������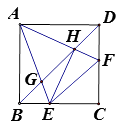
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϵ�A��Ӧ����Ϊ![]() ����B��Ӧ����Ϊ
����B��Ӧ����Ϊ![]() ���Ҷ���ʽ
���Ҷ���ʽ![]() �Ķ�����ϵ��Ϊ
�Ķ�����ϵ��Ϊ![]() ��������Ϊ
��������Ϊ![]() .
.
(1)ֱ��д��:![]() ��
��
(2)�����ϵ�A��B֮����һ����P������P��Ӧ����Ϊ![]() ���Ի���
���Ի���![]() ��
��
(3)����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ������������ƶ���ͬʱ��N�ӵ�B������������ÿ��2����λ���ȵ��ٶ������ƶ�������A����������ز����Ҽ����ƶ������������M��N�������1����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֻ�׳���5��5�ķ���(ÿС��߳�Ϊ1)�������������˶�������A����������B��C��D���������׳森�涨������������Ϊ��������������Ϊ���������A��B��Ϊ��A��B(��1����4)����B��A��Ϊ��B��A(��1����4)�����е�һ����ʾ���ҷ��ڶ�������ʾ���·�����ôͼ��

(1)A��C( �� )��B��D( �� )��
(2)����ֻ�׳������·��ΪA��B��C��D�������ü׳��߹���·�̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��
��1����ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
��2������P���߶�AB�ϣ���ͼ2������AC����PΪAB���е�ʱ���жϡ�ACE����״����˵������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com