
【题目】数学活动 实验、猜想与证明
问题情境
(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD中,AB=2BC,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.

解决问题
(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;
(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.
【答案】(1)MD=MC;(2)证明见解析;(3)∠BME=3∠AEM,证明见解析
【解析】
(1)根据矩形的性质可得AD=BC,∠A=∠B=90°,然后利用SAS证出△AMD≌△BMC,即可得出结论;
(2)根据平行四边形的判定证出四边形AMND和四边形MBCN为平行四边形,利用平行线分线段成比例定理证出CF=EF,从而得出MN垂直平分CE,根据垂直平分线的性质即可证出结论;
(3)根据平行四边形的性质可得AD∥MN∥BC,CF∥BM,MN=BC,然后根据平行线的性质、三线合一和等边对等角证出∠AEM=∠EMF、∠BMC=∠NMC、∠EMF=∠NMC,从而证出结论.
解:(1)MD=MC
∵四边形ABCD为矩形
∴AD=BC,∠A=∠B=90°
∵点M为AB的中点
∴AM=BM
在△AMD和△BMC中
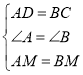
∴△AMD≌△BMC
∴MD=MC
(2)∵M,N分别是AB,CD的中点,
∴AM=BM,CN=DN
∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴AM=BM= CN=DN
∴四边形AMND和四边形MBCN为平行四边形
∴AD∥MN
∴![]()
∴CF=EF
∵CE⊥AD
∴CE⊥MN
∴MN垂直平分CE
∴ME = MC
(3)∠BME=3∠AEM,证明如下:
∵四边形AMND和四边形MBCN为平行四边形
∴AD∥MN∥BC,CF∥BM,MN=BC
∴∠AEM=∠EMF,∠NCM=∠BMC
∵AB=2BC,AB=CD=2CF
∴CF=MN
∴∠NCM=∠NMC
∴∠BMC=∠NMC
∵ME = MC,MF⊥CE
∴∠EMF=∠NMC
∴∠BME=∠EMF+∠NMC+∠BMC=3∠EMF=3∠AEM
即∠BME=3∠AEM


科目:初中数学 来源: 题型:
【题目】红红有两把不同的锁和四把不同的钥匙,其中只有两把钥匙能打开对应的两把锁,用列表法或树状图求概率.
(1)若取一把钥匙,求红红一次打开锁的概率;
(2)若取两把钥匙,求红红恰好打开两把锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在150≤x<175范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:

身高情况分组表
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高在155≤x<165之间的学生有18人;
②初一学生中女生的身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④初一学生身高在160≤x<170之间的学生约有800人.
其中合理的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,

(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)根据图象,直接写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
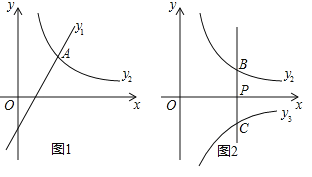
![]() 如图1,若
如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .求m,k的值;
.求m,k的值;
![]() 如图2,过点
如图2,过点![]() 作y轴的平行线l与函数
作y轴的平行线l与函数![]() 的图象相交于点B,与反比例函数
的图象相交于点B,与反比例函数![]() 的图象相交于点C.
的图象相交于点C.
![]() 若
若![]() ,直线l与函数
,直线l与函数![]() 的图象相交点
的图象相交点![]() 当点B、C、D中的一点到另外两点的距离相等时,求
当点B、C、D中的一点到另外两点的距离相等时,求![]() 的值;
的值;
![]() 过点B作x轴的平行线与函数
过点B作x轴的平行线与函数![]() 的图象相交与点
的图象相交与点![]() 当
当![]() 的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
查看答案和解析>>
科目:初中数学 来源: 题型:
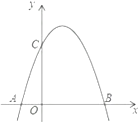
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,OC平分∠AOB,点P是射线OC上的一点.
,OC平分∠AOB,点P是射线OC上的一点.

(1)如图一,过点P作PD⊥OA,PE⊥OB,说明PD与PE相等的理由.
(2)如图二,如果点F、G分别在射线OA、OB上,且∠FPG=60°,那么线段PF与PG相等吗?请说明理由;
(3)在(2)的条件下,联合FG,![]() 是什么形状的三角形,请说明理由.
是什么形状的三角形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com