
����Ŀ����֪һ�κ���![]() �ͷ���������
�ͷ���������![]() ��
��
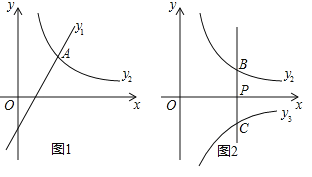
![]() ��ͼ1����
��ͼ1����![]() ���Һ���
���Һ���![]() ��
��![]() ��ͼ������
��ͼ������![]() ����m��k��ֵ��
����m��k��ֵ��
![]() ��ͼ2������
��ͼ2������![]() ��y���ƽ����l�뺯��
��y���ƽ����l�뺯��![]() ��ͼ���ཻ�ڵ�B���뷴��������
��ͼ���ཻ�ڵ�B���뷴��������![]() ��ͼ���ཻ�ڵ�C��
��ͼ���ཻ�ڵ�C��
![]() ��
��![]() ��ֱ��l�뺯��
��ֱ��l�뺯��![]() ��ͼ���ཻ��
��ͼ���ཻ��![]() ����B��C��D�е�һ�㵽��������ľ������ʱ����
����B��C��D�е�һ�㵽��������ľ������ʱ����![]() ��ֵ��
��ֵ��
![]() ����B��x���ƽ�����뺯��
����B��x���ƽ�����뺯��![]() ��ͼ���ཻ���
��ͼ���ཻ���![]() ��
��![]() ��ֵȡ������1������ʵ��ʱ����B��C��ľ������B��E��ľ���֮��dʼ����һ����ֵ�����ʱk��ֵ����ֵd��
��ֵȡ������1������ʵ��ʱ����B��C��ľ������B��E��ľ���֮��dʼ����һ����ֵ�����ʱk��ֵ����ֵd��
���𰸡���1��m=12��k=2����2����m-n=1��m-n=4����k=1����ֵd=1
��������
��1������A���������һ�κ�������ʽ������⣬����A��������뷴������������ʽ��������⣻
��2����BD��2+n��m��BC��m��n��DC��2+n��n��2����BD��BC��BD��DC��BC��CD�ã�m��n��1��0��2��������⣻
����E��������![]() ��m����d��BC+BE��m��n+��1��
��m����d��BC+BE��m��n+��1��![]() ����1+��m��n����1��
����1+��m��n����1��![]() ����������⣮
����������⣮
�⣺��1����n����2ʱ��y1��kx��2��
����A��3��4������һ�κ���y1��kx��2
�ã�3k��2��4��
��ã�k��2��
����A��3��4�����뷴���������ã�m��3��4��12��
��m��12��k��2��
��2������x��1ʱ����D��B��C������ֱ�Ϊ��1��2+n������1��m������1��n����
��BD��|2+n��m|��BC��m��n��DC��2+n��n��2
��BD��BC��BD��DC��BC��CD��
����|2+n��m|��m��n��|2+n��m|��2��m��n��2��
����m��n��1��0��2��4��
��m��n��0ʱ��m��n�����ⲻ����
��D������C���·�����BC��CDҲ�����ڣ�n+2��n����m��n��2��������
��m��n��1��m��n��4��
����E�ĺ�����Ϊ��![]() ��
��
����E�ڵ�B���ʱ��
d��BC+BE��m��n+��1��![]() ����1+��m��n����1��
����1+��m��n����1��![]() ����
����
m��n��ֵȡ������1��������ʱ��dʼ����һ����ֵ��
��1��![]() ��0ʱ����ʱk��1���Ӷ�d��1��
��0ʱ����ʱk��1���Ӷ�d��1��
����E�ڵ�B�Ҳ�ʱ��
ͬ��BC+BE����m��n����1+![]() ����1��
����1��
��1+![]() ��0��k����1ʱ��������������ȥ��
��0��k����1ʱ��������������ȥ��
��k��1��d��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�����ܻ����˽ӵ�����ָ���ԭ��O�����������ң����ϣ����ң����µķ������β����ƶ���ÿ���ƶ�1m��������·����ͼ��ʾ����1���ƶ���A1����2���ƶ���A2��������n���ƶ���An�����OA2A2018������ǣ�������
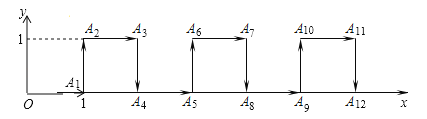
A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
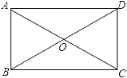
����Ŀ����ͼ������ABCD�У�AC��BD�ཻ�ڵ�O���� AO=3����OBC=30�㣬����ε��ܳ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ� ʵ�顢������֤��
�����龳
��1����ѧ����ϣ�Сӱ��ͬѧ�����������һ�����⣺��ͼ��1�����ھ���ABCD�У�AB=2BC��M��N�ֱ���AB��CD���е㣬������MN������MD��MC����ֱ��д���߶�MD��MC֮���������ϵ��

�������
��2��С���ܴ�����������������ABCD��Ϊƽ���ı��Σ����С�AΪ��ǣ���ͼ��2����AB=2BC��M��N�ֱ���AB��CD���е㣬����C��CE��AD������AD�ڵ�E��������MN�ڵ�F������ME��MC����ME=MC������֤��С��Ľ��ۣ�
��3��С����С����۵Ļ����������һ�������⣺��BME���AEM��������������ϵ������ش�С�������������⣬��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С������ѧ����С��ʱ��������һ�����⣺
![]()
���һ������ʽ�к��о���ֵ�����Ҿ���ֵ�����к���δ֪�������ǰ��������ʽ��������ֵ����ʽ�������ֵ����ʽ|x|��3�Ľ⼯��
С��ͬѧ��˼·���£�
�ȸ��ݾ���ֵ�Ķ��壬���|x|ǡ����3ʱx��ֵ�����������ϱ�ʾΪ��A��B����ͼ��ʾ���۲����ᷢ�֣��Ե�A��BΪ�ֽ��������Ϊ�����֣�
��A��ߵĵ��ʾ�����ľ���ֵ����3��
��A��B֮��ĵ��ʾ�����ľ���ֵС��3��
��B�ұߵĵ��ʾ�����ľ���ֵ����3��
��ˣ�С���ó����۾���ֵ����ʽ|x|��3�Ľ⼯Ϊ��x��-3��x��3��
����С����˼·������������⣺
��1������ֱ��д�����о���ֵ����ʽ�Ľ⼯��
��|x|��1�Ľ⼯�� ��
��|x|��2.5�Ľ⼯�� ��
��2�������ֵ����ʽ2|x-3|+5��13�Ľ⼯��
��3��ֱ��д������ʽx2��4�Ľ⼯�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ�������һ����������ת����ת�̣���ͼ��ʾ�����涨���˿�����200Ԫ����200Ԫ�����ϣ����ܻ��һ��ת��ת�̵Ļ��ᣬ���ת��ֹͣ��ָ�����ö����ۡ����ۡ��������˿;Ϳ��Ի�ô����Żݣ����ָ��ǡ���ڷָ�����ʱ����������ת��ת��.
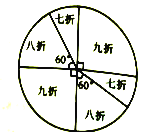
��1��ij�˿���������220Ԫ����תһ��ת�̣�����þ��ۡ����ۡ������Żݵĸ��ʷֱ��Ƕ��٣�
��2��ij�˿������л����ת��һ��ת�̵Ļ��ᣬʵ�ʸ���168Ԫ������������������Ʒ��ԭ��ӦΪ����Ԫ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��� x2-6x+m+4=0������ʵ���� x1��x2.
��1����m��ȡֵ��Χ��
��2���� x1��x2����x2-2x1=-3 ����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ�����������������ʦ�����ȡ��У������Ů�����г������飬��֪��ȡ�������У�������Ů��������ͬ�������������ݻ�������ͳ��ͼ����
��� | ���� |
|
|
|
|
|
|
|
|
|
|
������������
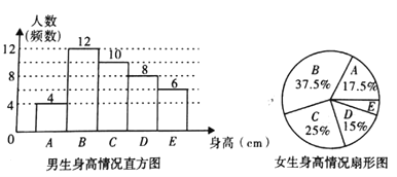
����ͼ���ṩ����Ϣ���ش��������⣺
��1�������У�Ů��������![]() ���������_________�ˣ�
���������_________�ˣ�
��2�������������ͳ��ͼ�У���ʾ![]() ������ε�Բ�Ľ���_________����
������ε�Բ�Ľ���_________����
��3����֪��У��������800�ˣ�Ů��760�ˣ�����Ƹ�У������![]() ֮���ѧ��Լ�ж����ˣ�
֮���ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���д�С���ֻ�����3���������2��С����һ�ο����˻�21�֣�2���������4��С����һ�ο����˻�22�֣�
��1��ÿ���������ÿ��С����һ�θ������˻����ٶ֣�
��2�����������ֻ�����10����Ҫ��һ���˻�������35�֣������д�������ٶ����������ò���ʽ���
��3����ǰ��23�ֻ�����Ҫ���䣬�����������ֻ������ͣ�Ҫ��ȫ������һ��������ÿ��������װ������֪ÿ�������һ���˻����Ϊ300Ԫ��ÿ��С����һ���˻����Ϊ200Ԫ�����г����е����䷽��������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com