
ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥–Θ―ß…ζΒΡ…μΗΏ«ιΩωΘ§Άθάœ ΠΥφΜζ≥ι»ΓΗΟ–ΘΡ–…ζΓΔ≈°…ζΫχ––≥ι―υΒς≤ιΘ§“―÷Σ≥ι»ΓΒΡ―υ±Ψ÷–Θ§Ρ–…ζΓΔ≈°…ζ»Υ ΐœύΆ§Θ§άϊ”ΟΥυΒΟ ΐΨίΜφ÷Τ»γœ¬Ά≥ΦΤΆΦ±μΘΚ
Ήι±π | …μΗΏ |
|
|
|
|
|
|
|
|
|
|
…μΗΏ«ιΩωΖ÷Ήι±μ
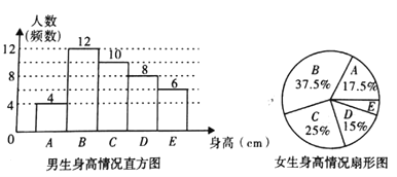
ΗυΨίΆΦ±μΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©―υ±Ψ÷–Θ§≈°…ζ…μΗΏ‘Ύ![]() ΉιΒΡ»Υ ΐ”–_________»ΥΘΜ
ΉιΒΡ»Υ ΐ”–_________»ΥΘΜ
Θ®2Θ©‘Ύ…œΟφΒΡ…»–ΈΆ≥ΦΤΆΦ÷–Θ§±μ Ψ![]() ΉιΒΡ…»–ΈΒΡ‘≤–ΡΫ« «_________ΓψΘΜ
ΉιΒΡ…»–ΈΒΡ‘≤–ΡΫ« «_________ΓψΘΜ
Θ®3Θ©“―÷ΣΗΟ–ΘΙ≤”–Ρ–…ζ800»ΥΘ§≈°…ζ760»ΥΘ§«κΙάΦΤΗΟ–Θ…μΗΏ‘Ύ![]() ÷°ΦδΒΡ―ß…ζ‘Φ”–Εύ…Ό»ΥΘΩ
÷°ΦδΒΡ―ß…ζ‘Φ”–Εύ…Ό»ΥΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©2ΘΜΘ®2Θ©18ΘΜΘ®3Θ©664»Υ
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σ≥ω≈°…ζ…μΗΏ‘ΎEΉιΥυ’ΦΒΡΑΌΖ÷±»Θ§‘Ό«σ≥ω≈°…ζΉή»Υ ΐ»ΜΚσœύ≥ΥΦ¥Ω…ΒΟΫβΘΜ
Θ®2Θ©”Ο360Γψ≥Υ“‘EΉιΥυ’ΦΒΡΑΌΖ÷±»Θ§Φ¥Ω…ΒΟΒΫ![]() ΉιΒΡ…»–ΈΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘΜ
ΉιΒΡ…»–ΈΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘΜ
Θ®3Θ©Ζ÷±π”ΟΡ–ΓΔ≈°…ζΒΡ»Υ ΐ≥Υ“‘CΓΔDΝΫΉιΒΡΤΒ¬ ΒΡΚΆΘ§ΦΤΥψΦ¥Ω…ΒΟΫβΘ°
ΫβΘΚΘ®1Θ©≈°…ζ…μΗΏ‘ΎEΉιΒΡΑΌΖ÷±»ΈΣΘΚ1-17.5%-37.5%-25%-15%=5%Θ§
ΓΏ≥ι»ΓΒΡ―υ±Ψ÷–Θ§Ρ–…ζΓΔ≈°…ζΒΡ»Υ ΐœύΆ§Θ§
Γύ―υ±Ψ÷–Θ§≈°…ζ…μΗΏ‘ΎEΉιΒΡ»Υ ΐ”–ΘΚ40ΓΝ5%=2Θ®»ΥΘ©Θ§
Ι ¥πΑΗΈΣΘΚ2
Θ®2Θ©EΉιΥυ‘Ύ…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐΈΣΘΚ360ΓψΓΝ5%=18Γψ
Ι ¥πΑΗΈΣΘΚ18
Θ®3Θ©![]() Θ®»ΥΘ©.
Θ®»ΥΘ©.
¥πΘΚΙάΦΤΗΟ–Θ…μΗΏ‘Ύ![]() ÷°ΦδΒΡ―ß…ζ‘Φ”–664»Υ.
÷°ΦδΒΡ―ß…ζ‘Φ”–664»Υ.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCDΆβ≤ύΘ§ΉςΒ»±Ώ»ΐΫ«–ΈADEΘ§ACΘ§BEœύΫΜ”ΎΒψFΘ§‘ρΓœCBFΈΣΘ®ΓΓΓΓΘ©
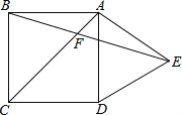
A.75ΓψB.60ΓψC.55ΓψD.45Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ“Μ¥ΈΚ· ΐ![]() ΚΆΖ¥±»άΐΚ· ΐ
ΚΆΖ¥±»άΐΚ· ΐ![]() Θ°
Θ°
![]() »γΆΦ1Θ§»τ
»γΆΦ1Θ§»τ![]() Θ§«“Κ· ΐ
Θ§«“Κ· ΐ![]() ΓΔ
ΓΔ![]() ΒΡΆΦœσΕΦΨ≠ΙΐΒψ
ΒΡΆΦœσΕΦΨ≠ΙΐΒψ![]() Θ°«σmΘ§kΒΡ÷ΒΘΜ
Θ°«σmΘ§kΒΡ÷ΒΘΜ
![]() »γΆΦ2Θ§ΙΐΒψ
»γΆΦ2Θ§ΙΐΒψ![]() Ήςy÷αΒΡΤΫ––œΏl”κΚ· ΐ
Ήςy÷αΒΡΤΫ––œΏl”κΚ· ΐ![]() ΒΡΆΦœσœύΫΜ”ΎΒψBΘ§”κΖ¥±»άΐΚ· ΐ
ΒΡΆΦœσœύΫΜ”ΎΒψBΘ§”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσœύΫΜ”ΎΒψCΘ°
ΒΡΆΦœσœύΫΜ”ΎΒψCΘ°
![]() »τ
»τ![]() Θ§÷±œΏl”κΚ· ΐ
Θ§÷±œΏl”κΚ· ΐ![]() ΒΡΆΦœσœύΫΜΒψ
ΒΡΆΦœσœύΫΜΒψ![]() Β±ΒψBΓΔCΓΔD÷–ΒΡ“ΜΒψΒΫΝμΆβΝΫΒψΒΡΨύάκœύΒ» ±Θ§«σ
Β±ΒψBΓΔCΓΔD÷–ΒΡ“ΜΒψΒΫΝμΆβΝΫΒψΒΡΨύάκœύΒ» ±Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
![]() ΙΐΒψBΉςx÷αΒΡΤΫ––œΏ”κΚ· ΐ
ΙΐΒψBΉςx÷αΒΡΤΫ––œΏ”κΚ· ΐ![]() ΒΡΆΦœσœύΫΜ”κΒψ
ΒΡΆΦœσœύΫΜ”κΒψ![]() Β±
Β±![]() ΒΡ÷Β»Γ≤Μ¥σ”Ύ1ΒΡ»Έ“β Β ΐ ±Θ§ΒψBΓΔCΦδΒΡΨύάκ”κΒψBΓΔEΦδΒΡΨύάκ÷°ΚΆd Φ÷’ «“ΜΗωΕ®÷ΒΘ°«σ¥Υ ±kΒΡ÷ΒΦΑΕ®÷ΒdΘ°
ΒΡ÷Β»Γ≤Μ¥σ”Ύ1ΒΡ»Έ“β Β ΐ ±Θ§ΒψBΓΔCΦδΒΡΨύάκ”κΒψBΓΔEΦδΒΡΨύάκ÷°ΚΆd Φ÷’ «“ΜΗωΕ®÷ΒΘ°«σ¥Υ ±kΒΡ÷ΒΦΑΕ®÷ΒdΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
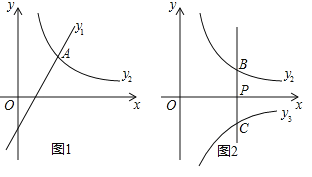
ΓΨΧβΡΩΓΩ»γΆΦΘ§ «ΫΪ≈ΉΈοœΏy=-x2 ΤΫ“ΤΚσΒΟΒΫΒΡ≈ΉΈοœΏΘ§ΤδΕ‘≥Τ÷αΈΣx=1Θ§”κx÷αΒΡ“ΜΗωΫΜΒψΈΣA(-1,0) Θ§Νμ“ΜΫΜΒψΈΣBΘ§”κy÷αΫΜΒψΈΣCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©»τΒψN ΈΣ≈ΉΈοœΏ…œ“ΜΒψΘ§«“BCΓΆNCΘ§«σΒψNΒΡΉχ±ξΘΜ
Θ®3Θ©ΒψP «≈ΉΈοœΏ…œ“ΜΒψΘ§ΒψQ «“Μ¥ΈΚ· ΐy=![]() x+
x+![]() ΒΡΆΦœσ…œ“ΜΒψΘ§»τΥΡ±Ώ–ΈOAPQΈΣΤΫ––ΥΡ±Ώ–ΈΘ§’β―υΒΡΒψPΓΔQ «Ζώ¥φ‘ΎΘΩ»τ¥φ‘ΎΘ§Ζ÷±π«σ≥ωΒψPΓΔQΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΆΦœσ…œ“ΜΒψΘ§»τΥΡ±Ώ–ΈOAPQΈΣΤΫ––ΥΡ±Ώ–ΈΘ§’β―υΒΡΒψPΓΔQ «Ζώ¥φ‘ΎΘΩ»τ¥φ‘ΎΘ§Ζ÷±π«σ≥ωΒψPΓΔQΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
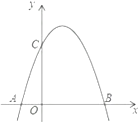
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςABCΘΚ
Θ®1Θ©«σΉςΓςABCΒΡΡΎ«–‘≤Γ―OΘ§”κ±ΏABΓΔBCΓΔACΖ÷±πœύ«–”ΎΒψDΓΔEΓΔFΘΜ
Θ®2Θ©»τAB=6Θ§BC=8Θ§AC=12Θ§«σADΓΔBEΓΔCFΒΡ≥ΛΕ».

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2019ΡξΈ“ ΓΩΣ’ΙΝΥ“‘ΓΑΗΡΗο¥¥–¬ΓΔΖήΖΔ”–ΈΣΓ±ΈΣ÷ςΧβΒΡ¥σΧ÷¬έΜνΕ·Θ§ΜνΕ·÷–Ρ≥…γ«χΈΣΝΥΒς≤ιΨ”ΟώΕ‘…γ«χΖΰΈώΒΡ¬ζ“βΕ»Θ§ΥφΜζ≥ι»ΓΝΥ…γ«χ≤ΩΖ÷Ψ”ΟώΫχ––Έ ΨμΒς≤ιΘΜ”Ο![]() ±μ ΨΓΑΚή¬ζ“βΓ±Θ§
±μ ΨΓΑΚή¬ζ“βΓ±Θ§![]() ±μ ΨΓΑ¬ζ“βΓ±Θ§
±μ ΨΓΑ¬ζ“βΓ±Θ§![]() ±μ ΨΓΑ±»Ϋœ¬ζ“βΓ±Θ§
±μ ΨΓΑ±»Ϋœ¬ζ“βΓ±Θ§![]() ±μ ΨΓΑ≤Μ¬ζ“βΓ±Θ§»γΆΦ «ΙΛΉς»Υ‘±ΗυΨίΈ ΨμΒς≤ιΆ≥ΦΤΉ ΝœΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ.
±μ ΨΓΑ≤Μ¬ζ“βΓ±Θ§»γΆΦ «ΙΛΉς»Υ‘±ΗυΨίΈ ΨμΒς≤ιΆ≥ΦΤΉ ΝœΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ.

«κΡψΗυΨίΆ≥ΦΤΆΦΧαΙ©ΒΡ–≈œΔΫβ¥π“‘œ¬Έ ΧβΘΚ
Θ®1Θ©±Ψ¥ΈΈ ΨμΒς≤ιΙ≤Βς≤ιΝΥΕύ…ΌΗωΨ”ΟώΘΩ
Θ®2Θ©«σ≥ωΒς≤ιΫαΙϊΈΣ![]() ΒΡ»Υ ΐΘ§≤ΔΫΪ÷±ΖΫΆΦ÷–
ΒΡ»Υ ΐΘ§≤ΔΫΪ÷±ΖΫΆΦ÷–![]() ≤ΩΖ÷ΒΡΆΦ–Έ≤Ι≥δΆξ’ϊΘΜ
≤ΩΖ÷ΒΡΆΦ–Έ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»γΙϊΗΟ…γ«χ”–Ψ”Οώ8000»ΥΘ§«κΡψΙάΦΤΕ‘…γ«χΖΰΈώΗ–ΒΫΓΑ≤Μ¬ζ“βΓ±ΒΡΨ”Οώ‘Φ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC ÷–Θ§ΒψO «AC±Ώ…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψOΉς÷±œΏMNΓΈBCΘ§…ηMNΫΜΓœBCAΒΡΫ«ΤΫΖ÷œΏ”ΎΒψEΘ§ΫΜΓœBCAΒΡΆβΫ«ΤΫΖ÷œΏ”ΎΒψF

Θ®1Θ©«σ÷ΛΘΚEO=FOΘΜ
Θ®2Θ©Β±ΒψO‘ΥΕ·ΒΫΚΈ¥Π ±Θ§ΥΡ±Ώ–ΈAECF «ΨΊ–ΈΘΩ≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() Θ§OCΤΫΖ÷ΓœAOB,ΒψP «…δœΏOC…œΒΡ“ΜΒψ.
Θ§OCΤΫΖ÷ΓœAOB,ΒψP «…δœΏOC…œΒΡ“ΜΒψ.

Θ®1Θ©»γΆΦ“ΜΘ§ΙΐΒψPΉςPDΓΆOAΘ§PEΓΆOBΘ§ΥΒΟςPD”κPEœύΒ»ΒΡάμ”….
Θ®2Θ©»γΆΦΕΰΘ§»γΙϊΒψFΓΔGΖ÷±π‘Ύ…δœΏOAΓΔOB…œΘ§«“ΓœFPG=60ΓψΘ§Ρ«Ο¥œΏΕΈPF”κPGœύΒ»¬πΘΩ«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΝΣΚœFG,![]() « ≤Ο¥–ΈΉ¥ΒΡ»ΐΫ«–ΈΘ§«κΥΒΟςάμ”….
« ≤Ο¥–ΈΉ¥ΒΡ»ΐΫ«–ΈΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΘ§““ΝΫΗω¥ϋ÷–ΨυΉΑ”–»ΐ’≈≥ΐΥυ±ξ ΐ÷ΒΆβΆξ»ΪœύΆ§ΒΡΩ®Τ§Θ§ΦΉ¥ϋ÷–ΒΡ»ΐ’≈Ω®Τ§…œΥυ±ξΒΡ»ΐΗω ΐ÷ΒΈΣ©¹7Θ§©¹1Θ§3Θ°““¥ϋ÷–ΒΡ»ΐ’≈Ω®Τ§…œΥυ±ξΒΡ ΐ÷ΒΈΣ©¹2Θ§1Θ§6Θ°œ»¥”ΦΉ¥ϋ÷–ΥφΜζ»Γ≥ω“Μ’≈Ω®Τ§Θ§”Οx±μ Ψ»Γ≥ωΒΡΩ®Τ§…œΒΡ ΐ÷ΒΘ§‘Ό¥”““¥ϋ÷–ΥφΜζ»Γ≥ω“Μ’≈Ω®Τ§Θ§”Οy±μ Ψ»Γ≥ωΒΡΩ®Τ§…œΒΡ ΐ÷ΒΘ§Α―xΘ§yΖ÷±πΉςΈΣΒψAΒΡΚαΉχ±ξΚΆΉίΉχ±ξΘ°
Θ®1Θ©”Ο Β±ΒΡΖΫΖ®–¥≥ωΒψAΘ®xΘ§yΘ©ΒΡΥυ”–«ιΩωΘΜ
Θ®2Θ©«σΒψA¬δ‘ΎΖ¥±»άΐΚ· ΐ![]() ΆΦœσ…œΒΡΗ≈¬ Θ°
ΆΦœσ…œΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com