Question

【题目】设函数f（x）=xex﹣ax（a∈R，a为常数），e为自然对数的底数． （Ⅰ）当f（x）＞0时，求实数x的取值范围；
（Ⅱ）当a=2时，求使得f（x）+k＞0成立的最小正整数k．

Answer 1

【答案】解：（Ⅰ）由f（x）＞0，可知x（ex﹣a）＞0， 当a≤0时，ex﹣a＞0，由x（ex﹣a）＞0，解得x＞0；
当0＜a≤1时，lna≤0，由x（ex﹣a）＞0，解得x＞0或x＜lna；
当a＞1时，lna＞0，由x（ex﹣a）＞0，解得x＞lna或x＜0；
（Ⅱ）当a=2时，要使f（x）+k＞0恒成立，即xex﹣2x＞﹣k恒成立．
令f（x）=xex﹣2x，则f′（x）=h（x）=（x+1）ex﹣2，h′（x）=（x+2）ex ．
当x∈（﹣∞，﹣2）时，h′（x）＜0，函数h（x）在（﹣∞，﹣2）上单调递减；
当x∈（﹣2，+∞）时，h′（x）＞0，函数h（x）在（﹣2，+∞）上单调递增．
又∵x∈（﹣∞，﹣1）时，h（x）＜0，且h（0）=﹣1＜0，h（1）=2e2﹣2＞0．
∴存在唯一的x0∈（0，1），使得 ．
当x∈（﹣∞，x0）时，f′（x）＜0，函数f（x）在（﹣∞，x0）上单调递减；
当x∈（x0 ， +∞）时，f′（x）＞0，函数f（x）在（﹣∞，x0）上单调递增．
∴当x=x0时，f（x）取最小值．
f（x0）= ．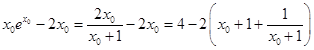
∵x0∈（0，1），∴f（x0）∈（﹣1，0）．
从而使f（x）+k＞0成立的最小正整数k的值为1．
【解析】（Ⅰ）由f（x）＞0，可知x（ex﹣a）＞0，然后对a分类求得实数x的取值范围；（Ⅱ）当a=2时，要使f（x）+k＞0恒成立，即xex﹣2x＞﹣k恒成立．构造函数f（x）=xex﹣2x，利用导数可得存在唯一的x0∈（0，1），使得当x∈（﹣∞，x0）时，f′（x）＜0，函数f（x）在（﹣∞，x0）上单调递减；当x∈（x0 ， +∞）时，f′（x）＞0，函数f（x）在（﹣∞，x0）上单调递增．由此可得当x=x0时，f（x）取最小值．从而使f（x）+k＞0成立的最小正整数k的值为1．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．