
【题目】若数列{an}是正项数列,且 ![]() +
+ ![]() +…+
+…+ ![]() =n2+3n(n∈N*),则
=n2+3n(n∈N*),则 ![]() +
+ ![]() +…+
+…+ ![]() = .
= .
科目:初中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax(a∈R,a为常数),e为自然对数的底数. (Ⅰ)当f(x)>0时,求实数x的取值范围;
(Ⅱ)当a=2时,求使得f(x)+k>0成立的最小正整数k.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强很喜欢操作探究问题,他把一条边长为8cm的线段AB放在直角坐标系中,使点A在y轴的正半轴上,点B在x轴的正半轴上,点P为线段AB的中点.在平面直角坐标系中进行操作探究:当点B从点O出发沿x轴正方向移动,同时顶点A随之从y正半轴上一点移动到点O为止.小强发现了两个正确的结论:
(1)点P到原点的距离始终是一个常数,则这个常数是_____cm;
(2)在B点移动的过程中,点P也随之移动,则点P移动的总路径长为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x+3|+|2x﹣1|. (Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1: ![]() 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: ![]() 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 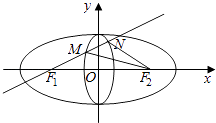
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1、用不超过16800元购进A、B两类图书共1000本; | |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
(1)发现:
△CMP和△BPA是否相似,若相似给出证明,若不相似说明理由;
(2)思考:
线段AM是否存在最小值?若存在求出这个最小值,若不存在,说明理由;
(3)探究:
当△ABP≌△ADN时,求BP的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com