
【题目】已知函数f(x)=(x2﹣3)ex , 设关于x的方程 ![]() 有n个不同的实数解,则n的所有可能的值为( )
有n个不同的实数解,则n的所有可能的值为( )
A.3
B.1或3
C.4或6
D.3或4或6
科目:初中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为 ![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两动圆F1:(x+ ![]() )2+y2=r2和F2:(x﹣
)2+y2=r2和F2:(x﹣ ![]() )2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足:
)2+y2=(4﹣r)2(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足: ![]()
![]() =0.
=0.
(1)求曲线C的方程;
(2)证明直线AB恒经过一定点,并求此定点的坐标;
(3)求△ABM面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)如果关于x的不等式|x+3|+|x﹣2|<a的解集不是空集,求参数a的取值范围; (Ⅱ)已知正实数a,b,且h=min{a, ![]() },求证:0<h≤
},求证:0<h≤ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数f(x)=xex﹣ax(a∈R,a为常数),e为自然对数的底数. (Ⅰ)当f(x)>0时,求实数x的取值范围;
(Ⅱ)当a=2时,求使得f(x)+k>0成立的最小正整数k.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,已知点P(0, ![]() ),曲线C的参数方程为
),曲线C的参数方程为 ![]() (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ= ![]() . (Ⅰ)判断点P与直线l的位置关系并说明理由;
. (Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强很喜欢操作探究问题,他把一条边长为8cm的线段AB放在直角坐标系中,使点A在y轴的正半轴上,点B在x轴的正半轴上,点P为线段AB的中点.在平面直角坐标系中进行操作探究:当点B从点O出发沿x轴正方向移动,同时顶点A随之从y正半轴上一点移动到点O为止.小强发现了两个正确的结论:
(1)点P到原点的距离始终是一个常数,则这个常数是_____cm;
(2)在B点移动的过程中,点P也随之移动,则点P移动的总路径长为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1: ![]() 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: ![]() 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 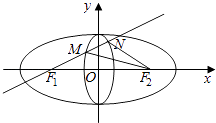
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体健康无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加添加剂2克,B饮料每瓶需加添加剂3克,饮料加工厂生产了A、B两种饮料各多少克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com