
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为 ![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
【答案】
(1)
解:由题意可知:椭圆的离心率e= ![]() =
= ![]() ,则a=
,则a= ![]() c,
c,
由△AOF的面积为S= ![]() ×b×c=
×b×c= ![]() ,则bc=1,
,则bc=1,
由a2=b2﹣c2,解得:a= ![]() ,b=c=1,
,b=c=1,
∴椭圆的标准方程为: ![]() ;
;
(2)
证明:由(1)可知:F(1,0),以椭圆的短轴为直径的圆的方程为x2+y2=1,
设P( ![]() cosθ,sinθ),且cosθ>0,则|PF|=
cosθ,sinθ),且cosθ>0,则|PF|= ![]() =
= ![]() =
= ![]() ﹣cosθ,
﹣cosθ,
由M是圆x2+y2=1的切点,则OM⊥PM,且丨OM丨=1,
则丨PM丨= ![]() =
= ![]() =
= ![]() =cosθ,
=cosθ,
∴|PF|+|PM|= ![]() ﹣cosθ+cosθ=
﹣cosθ+cosθ= ![]() ,
,
∴|PF|+|PM|为定值.
【解析】(1)根据椭圆的离心率求得a= ![]() c,bc=1,及a2=b2﹣c2 , 即可求得a和b的值,求得椭圆方程;(2)利用椭圆的参数方程,设P点坐标,利用两点之间的距离公式,及勾股定理即可求得:|PF|+|PM|的值为定值.
c,bc=1,及a2=b2﹣c2 , 即可求得a和b的值,求得椭圆方程;(2)利用椭圆的参数方程,设P点坐标,利用两点之间的距离公式,及勾股定理即可求得:|PF|+|PM|的值为定值.


科目:初中数学 来源: 题型:
【题目】如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F. 
(1)如图1,若BD=BA,求证:△ABE≌△DBE;
(2)如图2,若BD=4DC,取AB的中点G,连接CG交AD于M, 求证:①GM=2MC;
②AG2=AFAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2 ![]() ,DE=2,求AD的长,
,DE=2,求AD的长,
(3)在(2)的条件下,求弧BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(ω>0, ![]() )的部分图象如图所示,将函数f(x)的图象向右平移
)的部分图象如图所示,将函数f(x)的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间
个单位后得到函数g(x)的图象,若函数g(x)在区间 ![]() (
( ![]() )上的值域为[﹣1,2],则θ等于( )
)上的值域为[﹣1,2],则θ等于( ) 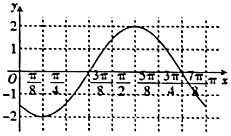
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A是抛物线y2=4x上的一点,以点A和点B(2,0)为直径的圆C交直线x=1于M,N两点.直线l与AB平行,且直线l交抛物线于P,Q两点. 
(Ⅰ)求线段MN的长;
(Ⅱ)若 ![]() =﹣3,且直线PQ与圆C相交所得弦长与|MN|相等,求直线l的方程.
=﹣3,且直线PQ与圆C相交所得弦长与|MN|相等,求直线l的方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且n+1=1+Sn对一切正整数n恒成立.
(1)试求当a1为何值时,数列{an}是等比数列,并求出它的通项公式;
(2)在(1)的条件下,当n为何值时,数列 ![]() 的前n项和Tn取得最大值.
的前n项和Tn取得最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣3)ex , 设关于x的方程 ![]() 有n个不同的实数解,则n的所有可能的值为( )
有n个不同的实数解,则n的所有可能的值为( )
A.3
B.1或3
C.4或6
D.3或4或6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com