Question

【题目】如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．
（1）如图1，若BD=BA，求证：△ABE≌△DBE；
（2）如图2，若BD=4DC，取AB的中点G，连接CG交AD于M， 求证：①GM=2MC；
②AG2=AFAC．

Answer 1

【答案】
（1）证明：在Rt△ABE和Rt△DBE中， ，

∴△ABE≌△DBE

（2）证明：①过G作GH∥AD交BC于H，

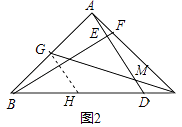
∵AG=BG，

∴BH=DH，

∵BD=4DC，

设DC=1，BD=4，

∴BH=DH=2，

∵GH∥AD，

∴ = = ，

∴GM=2MC；

②过C作CN⊥AC交AD的延长线于N，则CN∥AG，

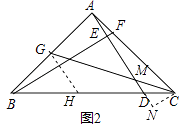
∴△AGM∽△NCM，

∴ = ，

由①知GM=2MC，

∴2NC=AG，

∵∠BAC=∠AEB=90°，

∴∠ABF=∠CAN=90°﹣∠BAE，

∴△ACN∽△BAF，

∴ = ，

∵AB=AG，

∴ = ，

∴2CNAG=AFAC，

∴AG2=AFAC．

【解析】（1）根据全等三角形的判定定理即可得到结论；（2）①过G作GH∥AD交BC于H，由AG=BG，得到BH=DH，根据已知条件设DC=1，BD=4，得到BH=DH=2，根据平行线分线段成比例定理得到 = = ，求得GM=2MC； ②过C作CN⊥AD交AD的延长线于N，则CN∥AG，根据相似三角形的性质得到 = ，由①知GM=2MC，得到2NC=AG，根据相似三角形的性质得到 = ，等量代换得到 = ，于是得到结论．
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．