
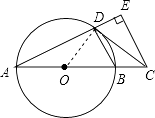
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2 ![]() ,DE=2,求AD的长,
,DE=2,求AD的长,
(3)在(2)的条件下,求弧BD的长。
【答案】
(1)
证明:连接OD,
∵CD是⊙O切线,
∴∠ODC=90°,
即∠ODB+∠BDC=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
即∠ODB+∠ADO=90°,
∴∠BDC=∠ADO,
∵OA=OD,
∴∠ADO=∠A,
∴∠BDC=∠A.
(2)
解:(2)∵CE⊥AE,
∴∠E=∠ADB=90°,
∴DB∥EC,
∴∠DCE=∠BDC,
∵∠BDC=∠A,
∴∠A=∠DCE,
在Rt△CDE中,CE=2![]() ,DE=2,
,DE=2,
则tan∠DCE=![]() ,
,
∴∠DCE=30°,
∴∠A=∠DCE=30°,
在Rt△ACE中,AE=![]() =2
=2![]() =6,
=6,
∴AD=AE-DE=4.
(3)
解:在Rt△ABD中,∠A=30°,AB=![]() ×AD=
×AD=![]() ,则OB=
,则OB=![]() AB=
AB=![]() .
.
由(1)得∠BOD=2∠A=60°,
则弧BD的长为![]() =
=![]() .
.
【解析】(1)连接OD,由“切线的性质”和“直径所对的圆周角为直角”可证明得;
(2)可先证∠A=∠DCE,由tan∠DCE=![]() ,可解得∠DCE的度数,从而可得∠A的度数为30°,即可求出AE;
,可解得∠DCE的度数,从而可得∠A的度数为30°,即可求出AE;
(3)求出圆心角∠BOD的度数,和半径OB,即可求得.
【考点精析】根据题目的已知条件,利用圆周角定理和切线的性质定理的相关知识可以得到问题的答案,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动,某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |

(1)表中a= , b=;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第组;
(4)请估计该校七年级学生日阅读量不足1小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2 ![]() 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE= ![]() BC;
BC;
(3)猜想PF与EQ的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=x2+ax+b图像与x轴有2个交点,A(x1,0),B(x2,0);且0< x1<1;1< x2<2,那么(1)a的取值范围是;b的取值范围是;则(2) ![]() 的取值范围是.
的取值范围是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C’处;作∠BPC’的角平分线交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为 ![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx有两个极值点x1、x2 , 且x1<x2 , 若x1+2x0=3x2 , 函数g(x)=f(x)﹣f(x0),则g(x)( )
A.恰有一个零点
B.恰有两个零点
C.恰有三个零点
D.至多两个零点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)如果关于x的不等式|x+3|+|x﹣2|<a的解集不是空集,求参数a的取值范围; (Ⅱ)已知正实数a,b,且h=min{a, ![]() },求证:0<h≤
},求证:0<h≤ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com