Question

9．如图，在矩形ABCD中，点E在线段BC上，DF⊥AE，垂足为点F，DF=AB；

（1）如图1，求证：BC=AE
（2）如图2，连接DE，点G在线段AF上，∠FDE+2∠DGE=90°，点K是线段EG中点，求证：DE=2KF；
（3）如图3，在（2）的条件下，DH为△GDE的角平分线，DM⊥DH，交∠DGE的角平分线于点M，若DG=6，KF=2，求tan∠DMG的值．

Answer 1

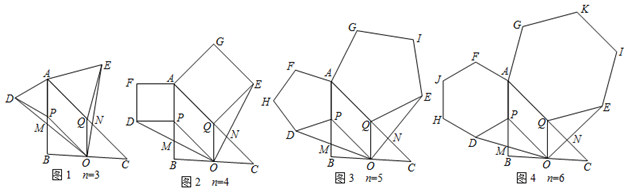
分析 （1）如图1中，连接DE．由DF=DC，DF⊥EA，DC⊥EC，推出∠DEC=∠DEF=∠ADE，推出AD=AE=BC．
（2）如图2中，在AF上取一点T，使得FT=EF．首先证明∠TGD=∠TDG，推出GT=DT=DE，推出DE=GT=GK+KT=KF+EF+KF-TF=2KF．
（3）首先证明∠M=∠DGE．设EF=a，则GK=KE=2+a，FG=4+a，因为∠DFE=∠DFG=90°，根据DF²=DG²-GF²=DE²-EF²，可得6²-（4+a）²=4²-a²，求出a=$\frac{1}{2}$，再根据tan∠DMG=tan∠DGF=$\frac{DF}{FG}$，求出DF、FG即可解决问题．

解答 （1）证明：如图1中，连接DE．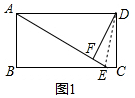

∵四边形ABCD是矩形，
∴AB=CD，AD=BC，∠B=∠C=90°，AD∥BC，
∴∠ADE=∠DEC
∵DF=AB，
∴DF=DC，
∵DF⊥EA，DC⊥EC，
∴∠DEC=∠DEF=∠ADE，
∴AD=AE=BC．

（2）证明：如图2中，在AF上取一点T，使得FT=EF．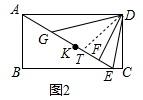

∵DF⊥ET，
∴DT=DE，
∴∠DTF=∠DET，∠FDT=∠FDE，
∵∠FDE+2∠DGE=90°，∠FDE+∠DEF=90°，
∴∠DTE=2∠DGE，
∵∠DTE=∠TGD+∠GDT，
∴∠TGD=∠TDG，
∴GT=DT=DE，
∵GK=KE，
∴DE=GT=GK+KT=KF+EF+KF-TF=2KF．

（3）解：如图3中，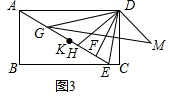

∵CM平分∠DGE，DH平分∠GDE，
∴∠FDG+∠FGD+$\frac{1}{2}$∠DEG=90°，
∵∠DFM=∠FDG+∠FGD，
∴∠DFM+$\frac{1}{2}$∠DEG=90°，
∵DM⊥DH，
∴∠MDH=90°，
∴∠M+∠DFM=90°，
∴∠M=$\frac{1}{2}$∠DEG，
由（2）可知，∠DGE=$\frac{1}{2}$∠DEG，DE=2FK=4，
∴∠M=∠DGE．设EF=a，则GK=KE=2+a，FG=4+a，
∵∠DFE=∠DFG=90°，
∴DF²=DG²-GF²=DE²-EF²，
∴6²-（4+a）²=4²-a²，
∴a=$\frac{1}{2}$，
∴FG=$\frac{9}{2}$，
在Rt△DFG中，DF=$\sqrt{D{G}^{2}-G{F}^{2}}$=$\sqrt{{6}^{2}-（\frac{9}{2}）^{2}}$=$\frac{3}{2}$$\sqrt{7}$，
∴tan∠DMG=tan∠DGF=$\frac{DF}{FG}$=$\frac{\frac{3}{2}\sqrt{7}}{\frac{9}{2}}$=$\frac{\sqrt{7}}{3}$．

点评 本题考查四边形综合题、角平分线的判定定理、三角形内角和、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造特殊三角形解决问题，属于中考压轴题．