
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
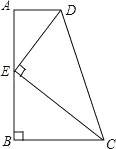
A.CE=![]() DE B.CE=
DE B.CE=![]() DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
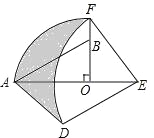
A.π B.![]() C.3+π D.8﹣π
C.3+π D.8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年参观“5.18”海交会的总人数约为489000人,将489000用科学记数法表示为( )
A.48.9×104
B.4.89×105
C.4.89×104
D.0.489×106
查看答案和解析>>
科目:初中数学 来源: 题型:
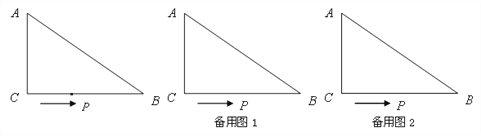
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
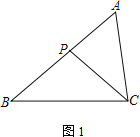
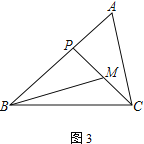
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com