
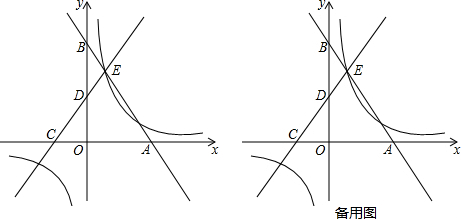
 实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切. 分析 根据$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,可以求得m的值,然后根据图中圆的圆心坐标和半径,可以求出圆心到直线的距离,然后与半径比较即可解答本题.
解答 解:∵$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,
∴a+c=mb,a+b=mc,b+c=ma,
∴2(a+b+c)=m(a+b+c),
得,m=2或a+b+c=0,
∴m=2或m=-1,
∴y=2x-$\sqrt{2}$或y=-x-$\sqrt{2}$,
∵图中⊙O的圆心坐标为(0,0),半径为1,
∴圆心到直线y=2x-$\sqrt{2}$的距离为:$\frac{|2×0-0-\sqrt{2}|}{\sqrt{{2}^{2}+(-1)^{2}}}$=$\frac{\sqrt{10}}{5}$,圆心到直线y=-x-$\sqrt{2}$的距离为:$\frac{|-0-0-\sqrt{2}|}{\sqrt{(-1)^{2}+(-1)^{2}}}=1$
∵$\frac{\sqrt{10}}{5}<1$,1=1,
∴直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
点评 本题考查直线与圆的位置关系.解题的关键是求出m的值,然后利用点到直线的距离公式求出圆心到直线的距离.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com