
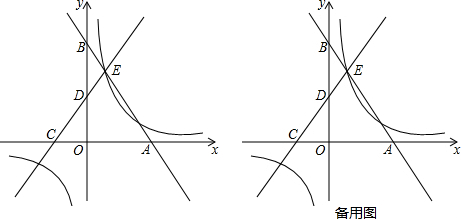
分析 (1)过点E作EF⊥y轴于点F,设EF=3x,则BF=4x,由勾股定理求出x的值可得出EF及BF的长,求出一元二次方程x2-17x+60=0的解可得出OA及OC的长,根据锐角三角函数的定义求出OB的长故可得出F点的坐标,求出E点坐标代入反比例函数的解析式可得出k的值;
(2)利用待定系数法求出直线AB的解析式,联立直线AB与反比例函数的解析式可得出P点坐标,再求出直线CD的解析式,利用S四边形ODEP=S梯形EFOA-S△DEF-S△OAP可得出结论;
(3)过点Q作QG⊥y轴,交直线CD于点G,设Q(m,$\frac{36}{m}$),则G($\frac{12}{m}$-5,$\frac{36}{m}$),得出QG的长,根据S△CEQ=$\frac{1}{2}$QG•(yE-yC)可得出m的值,进而得出Q点的坐标.
解答 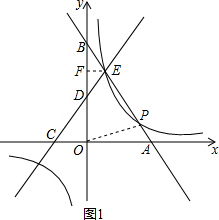 解:(1)如图1,过点E作EF⊥y轴于点F,
解:(1)如图1,过点E作EF⊥y轴于点F,
∵tan∠ABO=$\frac{3}{4}$,
∴tan∠EBF=$\frac{EF}{BF}$=$\frac{3}{4}$,
∴设EF=3x,则BF=4x.
∵BE=5,EF2+BF2=BE2,
∴(3x)2+(4x)2=52,解得x1=1,x2=-1(舍去),
∴EF=3,BF=4.
解一元二次方程x2-17x+60=0得x1=5,x2=12,
∵OA>OC,
∴OC=5,OA=12,
∴A(12,0),C(-5,0).
在Rt△ABO中,
∵BO=$\frac{AO}{tan∠ABO}$=$\frac{12}{\frac{3}{4}}$=16,
∴OF=16-4=12,
∴E(3,12),
将E(3,12)代入y=$\frac{k}{x}$得,k=36,
∴反比例函数的解析式为y=$\frac{36}{x}$;
(2)∵E(3,12),BF=4,
∴B(0,16).
设直线AB的解析式为y=kx+b(k≠0),
将A(12,0),B(0,16)代入得,
$\left\{\begin{array}{l}0=12k+b\\ 16=b\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{4}{3}\\ b=16\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{4}{3}$x+16,
∴$\left\{\begin{array}{l}y=-\frac{4}{3}x+16\\ y=\frac{36}{x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x}_{1}=3\\{y}_{1}=12\end{array}\right.$,$\left\{\begin{array}{l}{x}_{2}=9\\{y}_{2}=4\end{array}\right.$,
∴P(9,4).
设直线CD的解析式为y=ax+c(a≠0),
∵C(-5,0),(3,12),
∴$\left\{\begin{array}{l}0=-5a+c\\ 12=3a+c\end{array}\right.$,解得$\left\{\begin{array}{l}a=\frac{3}{2}\\ b=\frac{15}{2}\end{array}\right.$,
∴D(0,$\frac{15}{2}$),
∴S四边形ODEP=S梯形EFOA-S△DEF-S△OAP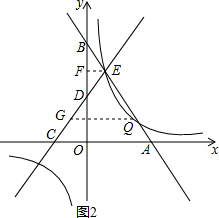 =$\frac{(3+12)×12}{2}$-$\frac{1}{2}$×3×(12-$\frac{15}{2}$)-$\frac{1}{2}$×12×4
=$\frac{(3+12)×12}{2}$-$\frac{1}{2}$×3×(12-$\frac{15}{2}$)-$\frac{1}{2}$×12×4
=$\frac{237}{4}$;
(3)存在.
如图2,过点Q作QG⊥y轴,交直线CD于点G,
∵设Q(m,$\frac{36}{m}$),则G($\frac{12}{m}$-5,$\frac{36}{m}$),
∴QG=m-($\frac{12}{m}$-5)=m-$\frac{12}{m}$+5,
∴S△CEQ=$\frac{1}{2}$QG•(yE-yC)=$\frac{1}{2}$×(m-$\frac{12}{m}$+5)×12=42,
解得m1=6,m2=-4,
∴Q(6,6)或Q(-4,-9).
点评 本题考查的是反比例函数综合题,涉及到利用待定系数求一次函数及反比例函数的解析式,锐角三角函数的定义等知识,在解答此题时要注意作出辅助线,构造出三角形求解.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
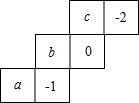 已知一个正方体包装盒的相对面上的数字是互为相反数,它的表面展开图如图所示,那么a、b、c对应的三个数依次是( )
已知一个正方体包装盒的相对面上的数字是互为相反数,它的表面展开图如图所示,那么a、b、c对应的三个数依次是( )| A. | 0,2,1 | B. | 0,1,-2 | C. | 1,0,-2 | D. | -2,0,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×104 | B. | 1.2×105 | C. | 0.12×106 | D. | 1.2×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,草原上有4口油井,位于四边形ABCD的4个顶点上,现要建一个维修站H,试问维修站H建在何处,才能使它到4口井的距离之和HA+HB+HC+HD为最小?试说明理由.
如图,草原上有4口油井,位于四边形ABCD的4个顶点上,现要建一个维修站H,试问维修站H建在何处,才能使它到4口井的距离之和HA+HB+HC+HD为最小?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗?
一块模板形状如图,按规定,AB,CD的延长线的交角为85°,因交点不在模板上,不便测量,于是工人师傅连结AC,方便地测出了AB,CD的延长线相交所成的角,工人师傅是如何测量的?这块模板符合规定吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.
实数a、b、c、m满足:$\frac{a+c}{b}$=$\frac{a+b}{c}$=$\frac{b+c}{a}$=m,那么直线y=mx-$\sqrt{2}$与如图中⊙O的位置关系为相交或相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com