
【题目】如图1,抛物线C1:y=ax2+bx+1的顶点坐标为D(1,0)且经过点(0,1),将抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,直线y=x+c,经过点D交y轴于点A,交抛物线C2于点B,抛物线C2的顶点为P.
(1)求抛物线C1的解析式;
(2)如图2,连结AP,过点B作BC⊥AP交AP的延长线于C,设点Q为抛物线上点P至点B之间的一动点,连结BQ并延长交AC于点F,
①当点Q运动到什么位置时,S△PBD×S△BCF=8?
②连接PQ并延长交BC于点E,试证明:FC(AC+EC)为定值.
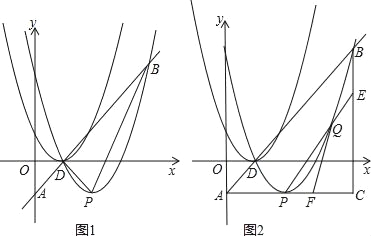
【答案】(1)y=x2﹣2x+1;(2)点Q运动到x轴时,S△PBD×S△BCF=8;②证明见解析.
【解析】
(1)已知顶点D的坐标,设抛物线的顶点式为:y=a(x-1)2,将点(0,1)代入即可;
(2)根据平移规律求出平移后抛物线的顶点坐标,即P(2,-1),根据顶点式,得平移后抛物线解析式y=(x-2)2-1,由解析式,得A(0,-1),B(4,3),可求△DBP的面积;
(3)由QM∥CE,得△PQM∽△PEC,利用相似比求EC,由QN∥FC,得△BQN∽△BFC,利用相似比求FC,已知AC=4,再计算FC(AC+EC)为定值.
(1)把顶点坐标为D(1,0)和点(0,1)坐标代入y=ax2+bx+1,
解得:抛物线的方程为:y=x2﹣2x+1;
(2)抛物线C1向右平移1个单位,向下平移1个单位得到抛物抛物线C1向右平移1个单位,向下平移1个单位得到抛物线C2,
则抛物线C2的方程为:y=(x﹣2)2﹣1=x2﹣4x+3,
此时顶点P坐标为(2,﹣1),A(0,﹣1)、B(4,3),
①则:S△PBD=3,S△BCF=![]() ,
,
设点Q(m,m2﹣4m+3),把Q、B点坐标代入一次函数表达式,
解得:BQ所在的直线方程为:y=mx+(3﹣4m),
则:F(![]() ,﹣1),S△BCF=
,﹣1),S△BCF=![]() FC(yB﹣yC)=
FC(yB﹣yC)=![]() =
=![]() ,
,
则m=3,点Q坐标为:(3,0),即:点Q运动到x轴时,S△PBD×S△BCF=8;
②如下图所示,过Q点分别作AC、BC的垂线QM、QN,

设:Q(t,t2﹣4t+3),则QM=CN=(t﹣2)2,MC=QN=4﹣t,
∵QM∥CE,∴![]() =
=![]() ,则:
,则:![]() =
=![]() ,解得:EC=2t﹣4,
,解得:EC=2t﹣4,
∵QN∥FC,![]() ,则:FC=
,则:FC=![]() ,而AC=4,
,而AC=4,
∴FC(AC+EC)=![]() (4+2t﹣4)=8,为定值.
(4+2t﹣4)=8,为定值.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
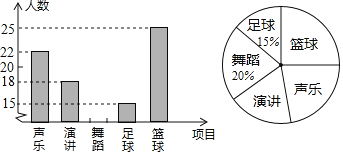
【题目】为丰富学生的文体生活,育红学校准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生一共有多少人?
(2)将条形统计图补充完整.
(3)若全校有学生1500人,请你估计全校有意参加“声乐”社团的学生人数.
(4)从被抽查的学生中随意选出1人,该学生恰好选择参加“演讲”社团的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
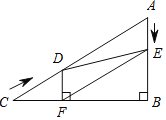
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
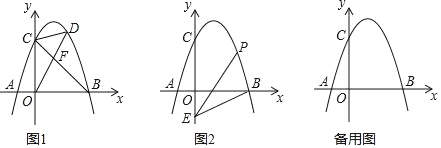
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式.
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
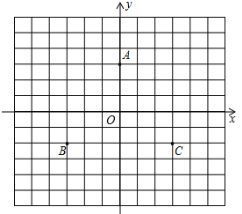
(1)图中点![]() 的坐标是________.
的坐标是________.
(2)点![]() 关于
关于![]() 轴对称的点
轴对称的点![]() 的坐标是______,并作出四边形
的坐标是______,并作出四边形![]() .
.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=![]() x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
x2+bx﹣2与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.且点A的坐标是(﹣1,0).
(1)求该抛物线的函数表达式及顶点D的坐标;
(2)判断△ABC的形状,并求出△ABC的面积;
(3)将抛物线向左或向右平移,得到抛物线L′,L′与x轴相交于A'、B′两点(点A′在点B′的左侧),并与y轴相交于点C′,要使△A'B′C′和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
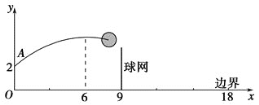
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com