
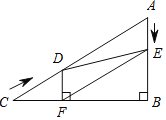
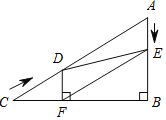
����Ŀ����ͼ����Rt��ABC�У���B��90����AC��60cm����A��60������D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE��DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
���𰸡���1������������2���ܣ�10����3����t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����
��������
��1������t��ʾ��CD�Լ�AE�ij���Ȼ����ֱ�ǡ�CDF�У�����ֱ�������ε��������DF�ij�������֤����
��2����֤�ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ��ݴ˼����з������t��ֵ��
��3���ֱ�ӡ�EDF��90�����DEF��90������������ۼ������.
��1��֤��������Rt��ABC�У���B��90����AC��60cm����A��60����
���C��90������A��30����
��CD��4tcm��AE��2tcm��
�֡���ֱ�ǡ�CDF�У���C��30����
��DF��![]() CD��2tcm��
CD��2tcm��
��DF��AE��
��2���ܣ�
��DF��AB��DF��AE��
���ı���AEFD��ƽ���ı��Σ�
��AD��AEʱ���ı���AEFD�����Σ�
��60��4t��2t��
��ã�t��10��
����t��10ʱ��AEFD�����Σ�
��3���⣺��t��![]() ʱ��DEF��ֱ�������Σ���EDF��90������
ʱ��DEF��ֱ�������Σ���EDF��90������
��t��12ʱ����DEF��ֱ�������Σ���DEF��90������
�������£�
����EDF��90��ʱ��DE��BC��
���ADE����C��30����
��AD��2AE
��CD��4tcm��
��DF��AE��2tcm��
��AD��2AE��4tcm��
��4t+4t��60��
��t��![]() ʱ����EDF��90����
ʱ����EDF��90����
����DEF��90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı��Σ�
��AD��EF��
��DE��AD��
���ADE��ֱ�������Σ���ADE��90����
�ߡ�A��60����
���DEA��30����
��AD��![]() AE��
AE��
AD��AC��CD��60��4t��cm����AE��DF��![]() CD��2tcm��
CD��2tcm��
��AD=tcm��
��60��4t��t��
���t��12��
������������t��![]() ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.
ʱ��DEF��ֱ�������Σ���EDF��90��������t��12ʱ����DEF��ֱ�������Σ���DEF��90����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�о�ѧ���Ŀ��మ���������ȡ��������ķ��������Ķ����˶������֡��������ĸ����������������ѧ������Ȥ���ã��������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
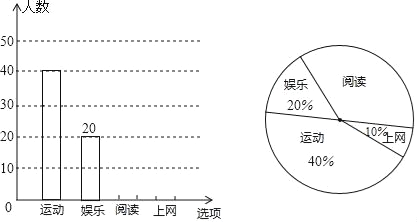
��1������ε����У�һ���������� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3������У����1500��ѧ�������ư����˶���ѧ������ ���ˣ�
��4����ȫУͬѧ�����ѡȡһ��ѧ���μ��ݽ���������Ƶ�ʹ��Ƹ��ʣ���ѡ����ǡ���ǰ����Ķ���ѧ���ĸ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�۲����
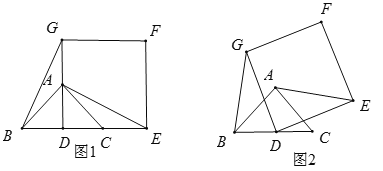
��ͼ(1)���ڡ�ABC�У���BAC=90�㣬AB=AC,��D��BC���е㣮�Ե�DΪ������������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG�����߶�BG��AE��������ϵ��_____��
(2)��չ̽��
��������DEFG�Ƶ�D��ʱ�뷽����תһ���ǶȺ���ת�Ƕȴ���0����С�ڻ����360��������ͼ2����(1)�еĽ����Ƿ���Ȼ���������������������֤�����������������˵������.
(3)�������
��BC=DE=2����(2)����ת�����У���AEΪ���ֵʱ��ֱ��д��AF��ֵ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ AB �ǡ�O ��ֱ������ C��D �ڡ�O �ϣ��� D ���� PF��AC����O �� F���� AB �ڵ� E����BPF=��ADC
��1����֤��AEEB=DEEF��
��2����֤��BP �ǡ�O �����ߣ�
��3�����İ뾶Ϊ![]() ��AC=2��BE=1 ʱ���� BP �ij���
��AC=2��BE=1 ʱ���� BP �ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������е�Ӱ�죬4�³�ij������۸������µ����µ���ÿ������۸���ԭ�۸��![]() ��ԭ����60Ԫ�������µ���ɶ���2�4����Ѯ����ר���о�֤ʵ�������в���������Ⱦ���ܿ����Ϊ����H1N1���У���ˣ�����۸�4�µ�ʼ���������������º�����۸��ϵ�Ϊÿ��14��4Ԫ��
��ԭ����60Ԫ�������µ���ɶ���2�4����Ѯ����ר���о�֤ʵ�������в���������Ⱦ���ܿ����Ϊ����H1N1���У���ˣ�����۸�4�µ�ʼ���������������º�����۸��ϵ�Ϊÿ��14��4Ԫ��
��1����4�³�����۸��µ���ÿ�����Ԫ��
��2����5��6�·�����۸����ƽ�������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
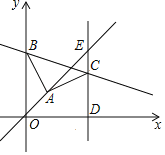
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�![]() ��
��![]() Ϊ
Ϊ![]() ����������һ�㣬����
����������һ�㣬����![]() ���ڵ�һ������
���ڵ�һ������![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����ֱ��
����ֱ��![]() ����ʽΪ____________��
����ʽΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣺����ֱ��������ABC�У���֪���߳�Ϊ3��4��������߳�Ϊ5���������ε�����a��b��c����a2+c2��b2�����C��90�����ۡ�ABC�У�����A����B����C��1��5��6�����ABC��ֱ�������Σ��ܡ�ABC�У���a��b��c��1��2��![]() ���������������ֱ�������Σ����У���ȷ����Ϊ_____��ѡ����ţ���
���������������ֱ�������Σ����У���ȷ����Ϊ_____��ѡ����ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC=90����AC=2AB����D��AC���е㣮��һ�����Ϊ45����ֱ�����ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�����BE��EC��
 �Բ����߶�BE��EC��������λ�ù�ϵ����֤����IJ��룮
�Բ����߶�BE��EC��������λ�ù�ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·���£�С����������ͼ���߶�AB��ʾ�����ڵ����ϵ�Ӱ����ͼ���߶�AC��ʾ��С����������ͼ���߶�FG��ʾ��·�Ƶ������߶�DE�ϣ�

��1������ȷ���������ڵ�λ�ã�������С���ڵƹ����γɵ�Ӱ�ӣ�
��2�����С��������AB=1.6m������Ӱ�ӳ�AC=1.4m��������·�Ƶľ���AD=2.1m������ݵĸ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com