
【题目】观察思考:

(1)在∠AOB内部画1条射线OC,则图中有3个不同的角;
(2)在∠AOB内部画2条射线OC、OD,则图中有几个不同的角?
(3)3条射线呢?你能发现什么规律,表示出n条射线能有几个不同的角?
请你先解答以上问题,再结合已学过的知识,针对类似的图形也提出三个问题并作答.(要求:画出图形,写出题干,提出问题并作答)
【答案】(2)6;(3)10;有![]() 个不同的角;提出三个问题并作答见解析.
个不同的角;提出三个问题并作答见解析.
【解析】
(2)根据图1直接数出即可;
(3)在图1的基础上看增加的角的个数即得画3条射线时角的个数;依此规律可得在∠AOB内部画n条射线时角的个数;把角换成线段,增加的射线条数换成线段上点的个数解答即可.
解:(2)在∠AOB内部画2条射线OC、OD,如图1,则图中有∠AOC、∠AOD、∠AOB、∠COD、∠COB、∠DOB共1+2+3=6个不同的角;
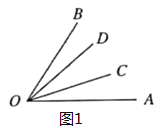
(3)在∠AOB内部画3条射线OC、OD、OE,如图2,在图1 的基础上增加了∠AOE、∠COE、∠DOE和∠BOE,共有6+4=10个不同的角;
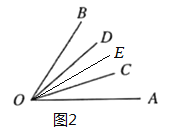
若在∠AOB内部画n条射线,则有![]() 个不同的角.
个不同的角.
提出问题:
(1)如图3,线段AB上有一个点C,则图3中共有 条不同的线段;
(2)如图4,线段AB上有两个点C、D,则图中共有几条不同的线段?
(3)线段AB上有3个点呢?你能发现什么规律,表示出线段AB上有n个点时能有几条不同的线段?
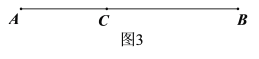

解:(1)图3中有:AC、AB、CB共3条不同的线段;
故答案为:3;
(2)如图4,图中有:AC、AD、AB、CD、CB、DB共1+2+3=6条线段;
(3)线段AB上有3个点C、D、E时,如图5,在图4的基础上增加了线段AE、BE、CE和DE,共有6+4=10条不同的线段;
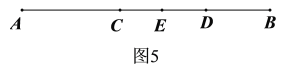
线段AB上有n个点时,则有![]() 条不同的线段.
条不同的线段.


科目:初中数学 来源: 题型:
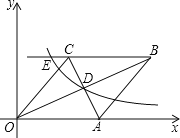
【题目】已知如图,四边形OABC为菱形,A点的坐标为![]() ,对角线OB、AC相交于D点,双曲线
,对角线OB、AC相交于D点,双曲线![]() 经过D点,交BC的延长线于E点,且
经过D点,交BC的延长线于E点,且![]() ,则E点的坐标是
,则E点的坐标是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“莓好莒南 幸福家园”---2018年莒南县第三届草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠,优惠期间,设某游客的草莓采摘量为![]() 千克
千克![]() ,在甲采摘园所需总费用为
,在甲采摘园所需总费用为![]() 元
元![]() ,在乙采摘园所需总费用为
,在乙采摘园所需总费用为![]() 元
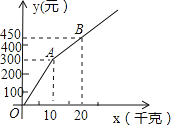
元![]() ,图中折线OAB表示
,图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.
![]() 求
求![]() ,
,![]() 与x的函数表达式;
与x的函数表达式;
![]() 若选择甲采摘园所需总费用较少,请求出草莓采摘量x的范围.
若选择甲采摘园所需总费用较少,请求出草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
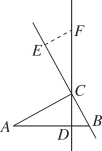
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
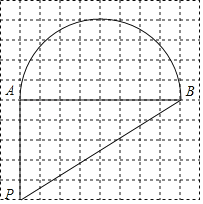
【题目】在每个小正方形的边长为1的网格中,有以AB为直径的半圆和线段AP,AB组成的一个封闭图形,点A,B,P都在网格点上.
(Ⅰ)计算这个图形的面积为_____;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一条能够将这个图形的面积平分的直线,并简要说明这条直线是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是平行四边形ABCD的边BC的中点,连接AE并延长交DC的延长线于点F,连接AC、BF,∠AEC=2∠ABC;(1)求证:四边形ABFC是矩形;(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
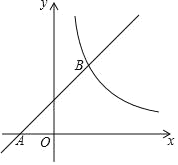
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=![]() (x>0)的图象交于B(a,4).
(x>0)的图象交于B(a,4).
(1)求一次函数和反比例函数的表达式;
(2)设M(m﹣2,m)是直线AB上一点,过M作MN∥x轴,交反比例函数y=![]() (x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
(x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com