
����Ŀ����֪������OABC��ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᣬy����������ϣ�����ֱ��������OEF��ֱ�Ƕ���O��ԭ�㣬E��F�ֱ���OA��OC�ϣ���OA��4��OE��2������OEF�Ƶ�O��ʱ����ת���á�OE1F1����E��F��ת��Ķ�Ӧ��ΪE1��F1��
������ͼ�٣���E1F1�ij�������ͼ�ڣ�����CF1��AE1����֤��OAE1�ա�OCF1��
������OEF�Ƶ�O��ʱ����תһ�ܣ���OE1��CF1ʱ�����E1�����ֱ꣨��д��������ɣ���

���𰸡�����2![]() ����֤��������������1��
����֤��������������1��![]() ����1����
����1����![]() ����
����
��������
�����ɵ���ֱ�������ε����ʺ��ɶ������EF��������ת�����ʼ��ɵó��𰸣��ڸ�����ת�������ҵ���ȵ��߶Σ�����SAS����֤����
�������ڡ�OEF�ǵ���Rt������OE��CF����ôCF����OF��ֱ������ת�����У�E��F�Ĺ켣����OΪԲ�ģ�OE����OF����Ϊ�뾶��Բ����CF��OF����ôCF��Ϊ��O�����ߣ����е�ΪF���ɹ�C����O�����ߣ���ô�������е㶼����F���Ҫ����˶�Ӧ��E��Ҳ����������Rt��OFC�У�OF��2��OC��OA��4����֤�á�FCO��30��������EOC��30������֪��OE�ij���ͨ����ֱ�������Σ��õ�E������꣬�ɴ˵ý⣮
���ٽ⣺�ߵ���ֱ��������OEF��ֱ�Ƕ���O��ԭ�㣬OE��2��
���EOF��90����OF��OE��2��
��EF��![]() ��
��![]() ��2
��2![]() ��
��
�߽���OEF�Ƶ�O��ʱ����ת���á�OE1F1��
��E1F1��EF��2![]() ��
��
��֤�������ı���OABCΪ�����Σ�
��OC��OA��
�߽���OEF�Ƶ�O��ʱ����ת���á�OE1F1��
���AOE1����COF1��
�ߡ�OEF�ǵ���ֱ�������Σ�
���OE1F1�ǵ���ֱ�������Σ�
��OE1��OF1��
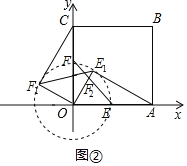
�ڡ�OAE1�͡�OCF1�У�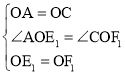
���OAE1�ա�OCF1��SAS����
���⣺��OE��OF��
�����F��OEƽ�е�ֱ������ֻ��һ��������OF��ֱ��
�����ǰ�OEF��O����ʱ����תһ��ʱ��
���F����OΪԲ�ģ���OFΪ�뾶��Բ�ϣ�
�����F��OF��ֱ��ֱ�߱���ԲO�����ߣ�
�ֵ�C��ԲO��һ�㣬����C��ԲO���е�ֱ������ֻ��2����������ΪCF1��CF2��
��ʱ��E��ֱ���E1���E2�㣬����CF1��OE1��CF2��OE2��
���е�F1�ڵڶ�����ʱ����E1�ڵ�һ���ޣ�
��ֱ��������CF1O�У�OC��4��OF1��2��
cos��COF1��![]() ��
��![]() ��
��![]() ��
��
���COF1��60����
���AOE1��60����
���E1�ĺ����ꣽ2cos60����1��
��E1�������ꣽ2sin60����![]() ��
��
���E1��������1��![]() ����
����
���е�F2�ڵ�һ����ʱ����E2�ڵ������ޣ�
ͬ������E2������Ϊ��1����![]() ����
����
������������OE1��CF1ʱ����E1������Ϊ��1��![]() ����1����
����1����![]() ����
����


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCD��90������BC��DC��ֱ��PQ������D������PDC������45��������135������BA��PQ�ڵ�A��������CA�Ƶ�C����ʱ�뷽����ת90������ֱ��PQ���ڵ�E��
��1��������125��ʱ����ABC���� ������
��2����֤��AC��CE��
��3������ABC�����������ڲ���ֱ��д������ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������OABC�Ƶ�O��ʱ����ת45����õ�������OA1B1C1�����˷�ʽ���Ƶ�O������ת2018�εõ�������OA2018B2018C2018�������A������Ϊ��1��0������ô��B2018������Ϊ��������
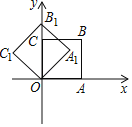
A. ��1��1�� B. ��0��![]() �� C. ��
�� C. ��![]() �� D. ����1��1��
�� D. ����1��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������з���Ͷ�ţ���������������������õ�Ч�ʣ�������Ⱦ������������Ϊ�˼�������������ʵ�����ij��ί������˼ס�����������飬��ȡ������ķ�ʽ�ֱ��Ͻ���ڵ�A��B��C��D�ĸ�С�����м�飬����ÿ��С�����ظ���飮
��1������鵽AС���ĸ����Ƕ��٣�
��2�������б�����״ͼ�ķ��������鵽AС����ͬʱ����鵽CС���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�У�ACΪֱ����MA��MB�ֱ��С�O�ڵ�A��B������B��BD��AC�ڵ�E������O�ڵ�D����BD��MA�����AMB�Ĵ�СΪ_____�ȣ�
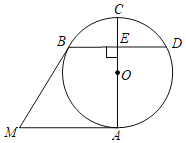
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
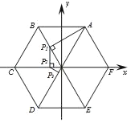
����Ŀ����ͼ������������ABCDEF������OΪԭ�㽨��ƽ��ֱ������ϵ������A��AP1��OB�ڵ�P1���ٹ�P1��P1P2��OC�ڵ�P2���ٹ�P2��P2P3��OD�ڵ�P3�����ν����������������εı߳�Ϊ1�����P2019�ĺ�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+3��x�ύ��A����1��0����B��3��0�����㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣬�ֱ�����AC��CD��AD��
��1���������ߵĺ�������ʽ�Լ�����D�����ꣻ
��2������������ȡһ��P�������C�غϣ������ֱ�����PA��PD������PAD���������ACD��������ʱ�����P�����ꣻ
��3������1��������õ���������A��D���ڵ�ֱ��ƽ�ƣ�ƽ�ƺ��A�Ķ�Ӧ��ΪA������C�Ķ�Ӧ��ΪC������D�Ķ�Ӧ��ΪD�������ı���AA��C��C������ʱ�����ʱƽ�ƺ�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
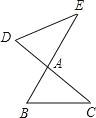
����Ŀ����ͼ��BE��CD �ཻ�ڵ� A������ BC��DE�����������в����жϡ�ABC��ADE ���ǣ� ��
A. ��B����D B. ��C����E C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��x2��2mx+m2��1��y�ύ�ڵ�C��
��1�����ú�m�Ĵ���ʽ��ʾ�����ߵĶ������ꣻ
��2����������y��x2��2mx+m2��1��ֱ��y����1���ۣ��õ�������������y�ύ�ڵ�D����m��0��CD��8����m��ֵ��
��3����֪A��2k��0����B��0��k�����ڣ�2���������£����߶�AB��������y��x2��2mx+m2��1ֻ��һ��������ʱ��ֱ��д��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com