
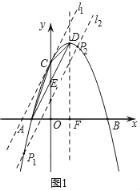
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+3гыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉКЭBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧИУХзЮяЯпЕФЖЅЕуЃЌЗжБ№СЌНгACЁЂCDЁЂADЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНвдМАЖЅЕуDЕФзјБъЃЛ
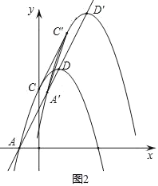
ЃЈ2ЃЉдкХзЮяЯпЩЯШЁвЛЕуPЃЈВЛгыЕуCжиКЯЃЉЃЌВЂЗжБ№СЌНгPAЁЂPDЃЌЕБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЪБЃЌЧѓЕуPЕФзјБъЃЛ
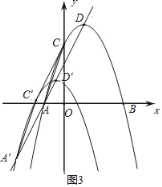
ЃЈ3ЃЉНЋЃЈ1ЃЉжаЫљЧѓЕУЕФХзЮяЯпбиAЁЂDЫљдкЕФжБЯпЦНвЦЃЌЦНвЦКѓЕуAЕФЖдгІЕуЮЊAЁфЃЌЕуCЕФЖдгІЕуЮЊCЁфЃЌЕуDЕФЖдгІЕуЮЊDЁфЃЌЕБЫФБпаЮAAЁфCЁфCЪЧСтаЮЪБЃЌЧѓДЫЪБЦНвЦКѓЕФХзЮяЯпЕФНтЮіЪНЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЌЃЈ1ЃЌ4ЃЉЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ
ЃЛЃЈ3ЃЉЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЃЎЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃН
ЃЉЃЎЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓЕУCЕФзјБъЃЌШЛКѓИљОнAЁЂBЕуЕФзјБъЩшХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНaЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌДњШыcЕФзјБъМДПЩЧѓЕУaЃЌЧѓЕУНтЮіЪНЃЌНјЖјЧѓЕУЖЅЕузјБъЃЛ
ЃЈ2ЃЉЯШЧѓЕУжБЯпADЕФНтЮіЪНЃЌШЛКѓЧѓЕУЯпЖЮADНЛyжсгкЕуEЕуЕФзјБъЃЌЙ§ЕуCзїжБЯпl1ЁЮADЃЌдђжБЯпl1ЕФНтЮіЪНЮЊyЃН2x+3ЃЌЧѓЕУгыХзЮяЯпЕФНЛЕуCЃЌгЩCЕФзјБъМДПЩХаЖЈдкЯпЖЮADЩЯЗНЕФХзЮяЯпЩЯВЛДцдкЪЙЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЕФЕуPЃЌНЋжБЯпADбиЪњжБЗНЯђЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЫљЕУЕФжБЯпl2ЕФНтЮіЪНЮЊyЃН2x+1ЃЎжБЯпl2гыХзЮяЯпНЛгкЕуPЃЌдђДЫЪБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЃЌСЊСЂЗНГЬМДПЩЧѓЕУНЛЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшAЁфЕФзјБъЮЊЃЈtЃЌ2t+2ЃЉЃЌдђЕУГіAЁфA2ЃН5ЃЈt+1ЃЉ2ЃЎAC2ЃН10ЃЎгЩЫФБпаЮAAЁфCЁфCЪЧСтаЮЃЌдђACЃНAAЁфЃЎДгЖјЕУГі5ЃЈt+1ЃЉ2ЃН10ЃЎНтЕУt1ЃН![]() Љ1ЃЌt2ЃНЉ
Љ1ЃЌt2ЃНЉ![]() Љ1ЃЌМДПЩЧѓЕУAЁфЕФзјБъЮЊЃЈ
Љ1ЃЌМДПЩЧѓЕУAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() Љ1ЃЌЉ2
Љ1ЃЌЉ2![]() ЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЧѓЕУМДПЩЃЎ
ЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЧѓЕУМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩХзЮяЯпyЃНax2+bx+3ПЩжЊCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЩшХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНaЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌ
ДњШыCЃЈ0ЃЌ3ЃЉЕУЉ3aЃН3ЃЎ
ЁрaЃНЉ1ЃЎ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНЉЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌМДyЃНЉx2+2x+3ЃЌ
ЁпЖдГЦжсЮЊжБЯпxЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
ДњШыЩЯЪНЃЌЕУyЃНЉЃЈ1+1ЃЉЃЈ1Љ3ЃЉЃН4ЃЎ
ЁрЖЅЕуDЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉЁпCЃЈ0ЃЌ3ЃЉЃЌOCЃН3ЃЎ
ЩшжБЯпADЕФНтЮіЪНЮЊyЃНkx+mЃЌдђ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁржБЯпADЕФНтЮіЪНЮЊyЃН2x+2ЃЌ
ЩшЯпЖЮADНЛyжсгкЕуEЃЌдђEЃЈ0ЃЌ2ЃЉЃЎ
ЁрCEЃНOCЉOEЃН3Љ2ЃН1ЃЎ
Й§ЕуCзїжБЯпl1ЁЮADЃЌдђжБЯпl1ЕФНтЮіЪНЮЊyЃН2x+3ЃЌШчЭМ1ЃЌ
гЩЉx2+2x+3ЃН2x+3ЃЌНтЕУx1ЃНx2ЃН0ЃЎ
НЋxЃН0ДњШыyЃН2x+3ЃЌЕУyЃН3ЃЎ
ЁржБЯпl1гыХзЮяЯпжЛгавЛИіНЛЕуCЃЎ
ЁрдкЯпЖЮADЩЯЗНЕФХзЮяЯпЩЯВЛДцдкЪЙЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЕФЕуPЃЌ
НЋжБЯпADбиЪњжБЗНЯђЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЫљЕУЕФжБЯпl2ЕФНтЮіЪНЮЊyЃН2x+1ЃЎ
жБЯпl2гыХзЮяЯпНЛгкЕуPЃЌдђДЫЪБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЃЎ
гЩЉx2+2x+3ЃН2x+1ЃЌНтЕУx1ЃН![]() ЃЌx2ЃНЉ
ЃЌx2ЃНЉ![]() ЃЎ
ЃЎ
Ёрy1ЃН2![]() +1ЃЌy2ЃНЉ2
+1ЃЌy2ЃНЉ2![]() +1ЃЎ
+1ЃЎ
ЁрЕуPЕФзјБъЮЊЃЈ![]() ЃЌ2
ЃЌ2![]() +1ЃЉЛђЃЈЉ
+1ЃЉЛђЃЈЉ![]() ЃЌЉ2
ЃЌЉ2![]() +1ЃЉЃЎ
+1ЃЉЃЎ
ЃЈ3ЃЉЩшAЁфЕФзјБъЮЊЃЈtЃЌ2t+2ЃЉЃЌ
дђAЁфA2ЃНЃЈt+1ЃЉ2+ЃЈ2t+2ЃЉ2ЃН5ЃЈt+1ЃЉ2ЃЎAC2ЃН12+32ЃН10ЃЎ
ЁпЫФБпаЮAAЁфCЁфCЪЧСтаЮЃЌ
ЁрACЃНAAЁфЃЎ
Ёр5ЃЈt+1ЃЉ2ЃН10ЃЎНтЕУt1ЃН![]() Љ1ЃЌt2ЃНЉ
Љ1ЃЌt2ЃНЉ![]() Љ1ЃЎ
Љ1ЃЎ
ЁрAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() Љ1ЃЌЉ2
Љ1ЃЌЉ2![]() ЃЉЃЎ
ЃЉЃЎ
ЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЃЎ
ЃЉЃЎ
НЋЕуAЯШЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2
ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2![]() ИіЕЅЮЛГЄЖШОЭЕУЕНЕуAЁфЃЌ
ИіЕЅЮЛГЄЖШОЭЕУЕНЕуAЁфЃЌ
ЁрНЋЕуDЃЈ1ЃЌ4ЃЉЯШЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2
ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2![]() ИіЕЅЮЛГЄЖШОЭЕУЕНЕуDЁфЃЈ
ИіЕЅЮЛГЄЖШОЭЕУЕНЕуDЁфЃЈ![]() +1ЃЌ2
+1ЃЌ2![]() +4ЃЉЃЎ
+4ЃЉЃЎ
ЁрЦНвЦКѓЕФХзЮяЯпЮЊyЃНЉЃЈxЉ![]() Љ1ЃЉ 2+4+2
Љ1ЃЉ 2+4+2![]() ЃЌ
ЃЌ
ЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃНЉЃЈxЉ1+![]() ЃЉ 2+4Љ2
ЃЉ 2+4Љ2![]() ЃЎ
ЃЎ


 бЇСЗПьГЕЕРПьРжМйЦкЪюМйзївЕаТНЎШЫУёГіАцЩчЯЕСаД№АИ
бЇСЗПьГЕЕРПьРжМйЦкЪюМйзївЕаТНЎШЫУёГіАцЩчЯЕСаД№АИ еуДѓгХбЇаЁбЇФъМЖЯЮНгЕМгыСЗеуНДѓбЇГіАцЩчЯЕСаД№АИ
еуДѓгХбЇаЁбЇФъМЖЯЮНгЕМгыСЗеуНДѓбЇГіАцЩчЯЕСаД№АИ аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ
аЁбЇЪюМйзївЕЖЋФЯДѓбЇГіАцЩчЯЕСаД№АИ НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЮЊФГИіОиаЮЕФСНИіЖЅЕуЃЌЧвИУОиаЮЕФБпОљгыФГЬѕзјБъжсДЙжБЃЎдђГЦИУОиаЮЮЊЕу
ЮЊФГИіОиаЮЕФСНИіЖЅЕуЃЌЧвИУОиаЮЕФБпОљгыФГЬѕзјБъжсДЙжБЃЎдђГЦИУОиаЮЮЊЕу![]() ЕФЯрЙиОиаЮ"ЃЎЯТЭМЮЊЕу
ЕФЯрЙиОиаЮ"ЃЎЯТЭМЮЊЕу![]() ЕФЁАЯрЙиОиаЮЁБЕФЪОвтЭМЃЎ
ЕФЁАЯрЙиОиаЮЁБЕФЪОвтЭМЃЎ
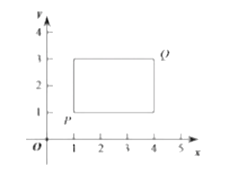
![]() вбжЊЕу
вбжЊЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
![]() ШєЕу
ШєЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФЁАЯрЙиОиаЮЁБЕФжмГЄЃЛ
ЕФЁАЯрЙиОиаЮЁБЕФжмГЄЃЛ
![]() Еу
Еу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌШєЕу
ЩЯЃЌШєЕу![]() ЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌвбжЊХзЮяЯп
ЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌвбжЊХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() КЭЕу
КЭЕу![]() ЃЌЧѓХзЮяЯп
ЃЌЧѓХзЮяЯп![]() гы
гы![]() жсЕФНЛЕу
жсЕФНЛЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФДгзѓЯђгвЕФвЛИіЖЏЕуЃЎШєдк
ЩЯЕФДгзѓЯђгвЕФвЛИіЖЏЕуЃЎШєдк![]() ЩЯДцдквЛЕу
ЩЯДцдквЛЕу![]() ЪЙЕУЕу
ЪЙЕУЕу![]() ЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌжБНгаДГіЖЏЕу
ЕФЁАЯрЙиОиаЮЁБЮЊе§ЗНаЮЃЌжБНгаДГіЖЏЕу![]() ЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГДѓаЭЦѓвЕЮЊСЫБЃЛЄЛЗОГЃЌзМБИЙКТђAЁЂBСНжжаЭКХЕФЮлЫЎДІРэЩшБИЙВ8ЬЈЃЌгУгкЭЌЪБжЮРэВЛЭЌГЩЗжЕФЮлЫЎЃЌШєЙКТђAаЭ2ЬЈЁЂBаЭ3ЬЈаш54ЭђЃЌЙКТђAаЭ4ЬЈЁЂBаЭ2ЬЈаш68ЭђдЊЃЎ
ЃЈ1ЃЉЧѓГіAаЭЁЂBаЭЮлЫЎДІРэЩшБИЕФЕЅМлЃЛ
ЃЈ2ЃЉОКЫЪЕЃЌвЛЬЈAаЭЩшБИвЛИідТПЩДІРэЮлЫЎ220ЖжЃЌвЛЬЈBаЭЩшБИвЛИідТПЩДІРэЮлЫЎ190ЖжЃЌШчЙћИУЦѓвЕУПдТЕФЮлЫЎДІРэСПВЛЕЭгк1565ЖжЃЌЧыФуЮЊИУЦѓвЕЩшМЦвЛжжзюЪЁЧЎЕФЙКТђЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЗНаЮOABCдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЃЌCЗжБ№дкxжсЃЌyжсЕФе§АыжсЩЯЃЌЕШбќжБНЧШ§НЧаЮOEFЕФжБНЧЖЅЕуOдкдЕуЃЌEЃЌFЗжБ№дкOAЃЌOCЩЯЃЌЧвOAЃН4ЃЌOEЃН2ЃЎНЋЁїOEFШЦЕуOФцЪБеыа§зЊЃЌЕУЁїOE1F1ЃЌЕуEЃЌFа§зЊКѓЕФЖдгІЕуЮЊE1ЃЌF1ЃЎ
ЃЈЂёЃЉЂйШчЭМЂйЃЌЧѓE1F1ЕФГЄЃЛЂкШчЭМЂкЃЌСЌНгCF1ЃЌAE1ЃЌЧѓжЄЁїOAE1ЁеЁїOCF1ЃЛ
ЃЈЂђЃЉНЋЁїOEFШЦЕуOФцЪБеыа§зЊвЛжмЃЌЕБOE1ЁЮCF1ЪБЃЌЧѓЕуE1ЕФзјБъЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаДѓаЁСНжжЛѕГЕЃЌ![]() СОДѓЛѕГЕгы
СОДѓЛѕГЕгы![]() СОаЁЛ№ГЕвЛДЮПЩвддЫЛѕ
СОаЁЛ№ГЕвЛДЮПЩвддЫЛѕ![]() ЖжЃЌ
ЖжЃЌ![]() СОДѓЛѕГЕгы
СОДѓЛѕГЕгы![]() СОаЁЛѕГЕвЛДЮПЩвддЫЛѕ
СОаЁЛѕГЕвЛДЮПЩвддЫЛѕ![]() Жж.
Жж.
ЃЈ1ЃЉЧѓ![]() СОДѓЛѕГЕКЭ
СОДѓЛѕГЕКЭ![]() СОаЁЛѕГЕвЛДЮПЩвдЗжБ№дЫЖрЩйЖжЃЛ
СОаЁЛѕГЕвЛДЮПЩвдЗжБ№дЫЖрЩйЖжЃЛ
ЃЈ2ЃЉЯжга![]() ЖжЛѕЮяашвЊдЫЪфЃЌЛѕдЫЙЋЫОФтАВХХДѓаЁЛѕГЕЙВ
ЖжЛѕЮяашвЊдЫЪфЃЌЛѕдЫЙЋЫОФтАВХХДѓаЁЛѕГЕЙВ![]() СОАбШЋВПЛѕЮявЛДЮдЫЭъ.ЧѓжСЩйашвЊАВХХМИСОДѓЛѕГЕЃП
СОАбШЋВПЛѕЮявЛДЮдЫЭъ.ЧѓжСЩйашвЊАВХХМИСОДѓЛѕГЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ШчЭМ1ЃЌвдЁїABCЕФБпABЮЊжБОЖзїЁбOЃЌНЛACгкЕуEЃЌBDЦНЗжЁЯABEНЛACгкFЃЌНЛдВOгкЕуDЃЌЧвЁЯBDE=ЁЯCBEЃЎ
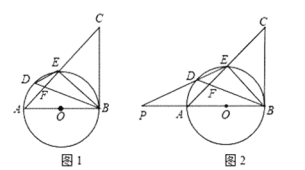
ЃЈ1ЃЉЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌбгГЄEDНЛжБЯпABгкЕуPЃЌШє PA=AOЃЌDE=2ЃЌЧѓ![]() ЕФжЕМАAOЕФГЄЃЎ
ЕФжЕМАAOЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЃжнЪаФГжабЇЬхг§ГЁПДЬЈЕФВрУцШчЭМвѕгАВПЗжЫљЪОЃЌПДЬЈгаЫФМЖИпЖШЯрЕШЕФаЁЬЈНзЃЎвбжЊПДЬЈИпЮЊ1.6УзЃЌЯжвЊзівЛИіВЛатИжЕФЗіЪж![]() МАСНИљгы
МАСНИљгы![]() ДЙжБЧвГЄЮЊ1УзЕФВЛатИжМмИЫ
ДЙжБЧвГЄЮЊ1УзЕФВЛатИжМмИЫ![]() КЭ
КЭ![]() (ИЫзгЕФЕзЖЫЗжБ№ЮЊ
(ИЫзгЕФЕзЖЫЗжБ№ЮЊ![]() )ЃЌЧв
)ЃЌЧв![]() ЃЌЧѓЫљгУВЛатИжВФСЯЕФзмГЄЖШЃЎ(МД
ЃЌЧѓЫљгУВЛатИжВФСЯЕФзмГЄЖШЃЎ(МД![]() ЃЌНсЙћОЋШЗЕН0.1Уз)ВЮПМЪ§Он(
ЃЌНсЙћОЋШЗЕН0.1Уз)ВЮПМЪ§Он(![]() )
)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
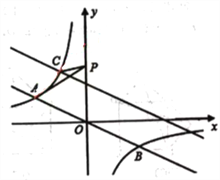
ЁОЬтФПЁПШчЭМЃЌжБНЧзјБъЯЕжаЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌвбжЊAЕуЕФзнзјБъЪЧ2.
ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌвбжЊAЕуЕФзнзјБъЪЧ2.
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪН.
ЃЈ2ЃЉНЋжБЯп![]() биxжсЯђгвЦНвЦ6ИіЕЅЮЛКѓЃЌгыЗДБШР§КЏЪ§дкЕкЖўЯѓЯоФкНЛгкЕуC.ЖЏЕуPдкyжсе§АыжсЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPCжЎВюДяЕНзюДѓЪБЃЌЧѓЕуPЕФзјБъ.
биxжсЯђгвЦНвЦ6ИіЕЅЮЛКѓЃЌгыЗДБШР§КЏЪ§дкЕкЖўЯѓЯоФкНЛгкЕуC.ЖЏЕуPдкyжсе§АыжсЩЯдЫЖЏЃЌЕБЯпЖЮPAгыЯпЖЮPCжЎВюДяЕНзюДѓЪБЃЌЧѓЕуPЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮЕФвЛЬѕБпГЄЮЊxЃЌжмГЄЕФвЛАыЮЊyЃЌЖЈвхЃЈxЃЌyЃЉЮЊетИіОиаЮЕФзјБъЁЃШчЭМ2ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпx=1ЃЌy=3НЋЕквЛЯѓЯоЛЎЗжГЩ4ИіЧјгђЃЌвбжЊОиаЮ1ЕФзјБъЕФЖдгІЕуAТфдкШчЭМЫљЪОЕФЫЋЧњЯпЩЯЃЌОиаЮ2ЕФзјБъЕФЖдгІЕуТфдкЧјгђЂмжаЃЌдђЯТУца№Ъіжае§ШЗЕФЪЧЃЈ ЃЉ

A. ЕуAЕФКсзјБъгаПЩФмДѓгк3
B. ОиаЮ1ЪЧе§ЗНаЮЪБЃЌЕуAЮЛгкЧјгђЂк
C. ЕБЕуAбиЫЋЧњЯпЯђЩЯвЦЖЏЪБЃЌОиаЮ1ЕФУцЛ§МѕаЁ
D. ЕБЕуAЮЛгкЧјгђЂйЪБЃЌОиаЮ1ПЩФмКЭОиаЮ2ШЋЕШ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com