
【题目】郑州市某中学体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手![]() 及两根与
及两根与![]() 垂直且长为1米的不锈钢架杆
垂直且长为1米的不锈钢架杆![]() 和
和![]() (杆子的底端分别为
(杆子的底端分别为![]() ),且
),且![]() ,求所用不锈钢材料的总长度.(即
,求所用不锈钢材料的总长度.(即![]() ,结果精确到0.1米)参考数据(
,结果精确到0.1米)参考数据(![]() )
)

科目:初中数学 来源: 题型:
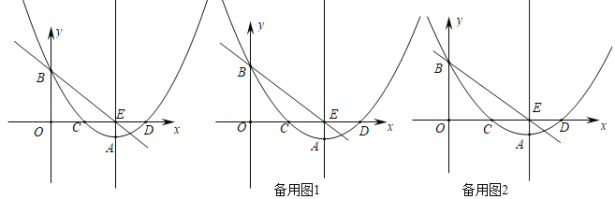
【题目】如图,一段抛物线:![]() ,记为
,记为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交
,交![]() 轴于点
轴于点![]() ;…,如此进行下去,直至得
;…,如此进行下去,直至得![]() .
.
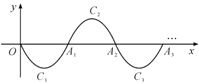
(1)请写出抛物线![]() 的解析式:________;
的解析式:________;
(2)若![]() 在第10段抛物线
在第10段抛物线![]() 上,则
上,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,则∠AMB的大小为_____度.
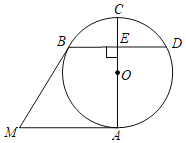
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.
(1)求抛物线的函数表达式以及顶点D的坐标;
(2)在抛物线上取一点P(不与点C重合),并分别连接PA、PD,当△PAD的面积与△ACD的面积相等时,求点P的坐标;
(3)将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
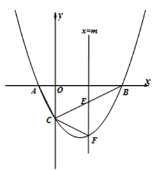
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
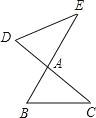
A. ∠B=∠D B. ∠C=∠E C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣11ax+24a交x轴于C,D两点,交y轴于点B(0,![]() ),过抛物线的顶点A作x轴的垂线AE,垂足为点E,作直线BE.
),过抛物线的顶点A作x轴的垂线AE,垂足为点E,作直线BE.
(1)求直线BE的解析式;
(2)点H为第一象限内直线AE上的一点,连接CH,取CH的中点K,作射线DK交抛物线于点P,设线段EH的长为m,点P的横坐标为n,求n与m之间的函数关系式.(不要求写出自变量m的取值范围);
(3)在(2)的条件下,在线段BE上有一点Q,连接QH,QC,线段QH交线段PD于点F,若∠HFD=2∠FDO,∠HQC=90°![]() ∠FDO,求n的值.
∠FDO,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线CF交BD延长线于点C.
(Ⅰ)若∠C=25°,求∠BAF的度数;
(Ⅱ)若AB=AC,CD=2,求AB的长.
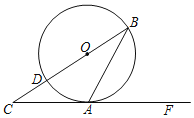
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com