
【题目】 如图1,以△ABC的边AB为直径作⊙O,交AC于点E,BD平分∠ABE交AC于F,交圆O于点D,且∠BDE=∠CBE.
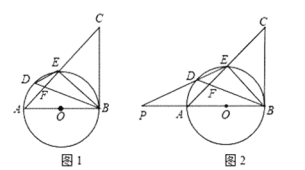
(1)求证:BC是⊙O的切线;
(2)如图2,延长ED交直线AB于点P,若 PA=AO,DE=2,求![]() 的值及AO的长.
的值及AO的长.
【答案】(1)详见解析;(2)![]() ;
;![]()
【解析】
(1)根据直径所对的圆周角是直角可得∠AEB=90°,从而得出∠A+∠EBA=90°,然后根据同弧所对的圆周角相等可得∠A=∠BDE,再结合已知条件即可证出∠CBA=90°,最后根据切线的判定定理即可证出结论;
(2)连接OD,根据圆周角定理可得∠DOP=2∠DBP,结合已知条件即可证出OD∥BE,再根据平行线分线段成比例定理即可求出![]() ,然后根据相似三角形的判定定理证出△APE∽△DPB,列出比例式即可求出结论.
,然后根据相似三角形的判定定理证出△APE∽△DPB,列出比例式即可求出结论.
(1)证明:∵AB为直径
∴∠AEB=90°
∴∠A+∠EBA=90°
∵∠A=∠BDE
∴∠BDE+∠EBA=90°
∵∠BDE=∠CBE
∴∠CBE+∠EBA=90°
∴∠CBA=90°
∴BC是⊙O的切线;
(2)解:连接OD,
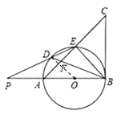
∴∠DOP=2∠DBP
∵BD平分∠ABE
∴∠EBP=2∠DBP
∴∠DOP=∠EBP
∴OD∥BE,
∴![]()
∵PA=AO=OB,
∴PO=2BO ,PB=3PA
∴![]()
∵DE=2
∴PD=2DE=4
∴PE=PD+DE=6
∵∠PEA=∠PBD,∠P=∠P
∴△APE∽△DPB,
∴![]()
∴![]()
解得:PA=![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对:物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以正六边形ABCDEF的中心O为原点建立平面直角坐标系,过点A作AP1⊥OB于点P1,再过P1作P1P2⊥OC于点P2,再过P2作P2P3⊥OD于点P3,依次进行……若正六边形的边长为1,则点P2019的横坐标为_____.
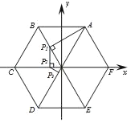
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.
(1)求抛物线的函数表达式以及顶点D的坐标;
(2)在抛物线上取一点P(不与点C重合),并分别连接PA、PD,当△PAD的面积与△ACD的面积相等时,求点P的坐标;
(3)将(1)中所求得的抛物线沿A、D所在的直线平移,平移后点A的对应点为A′,点C的对应点为C′,点D的对应点为D′,当四边形AA′C′C是菱形时,求此时平移后的抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”;
类表示“基本了解”;![]() 类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②):
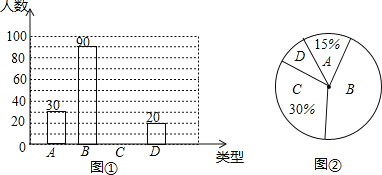
(1)在这次抽样调查中,一共抽查了 名学生;
(2)请把图①中的条形统计图补充完整;
(3)图②的扇形统计图中![]() 类部分所对应扇形的圆心角的度数为 ;
类部分所对应扇形的圆心角的度数为 ;
(4)如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
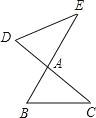
【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
A. ∠B=∠D B. ∠C=∠E C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线![]() (m≠0)向右平移
(m≠0)向右平移![]() 个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
个单位长度后得到抛物线G2,点A是抛物线G2的顶点.
(1)直接写出点A的坐标;
(2)过点(0,![]() )且平行于x轴的直线l与抛物线G2交于B,C两点.
)且平行于x轴的直线l与抛物线G2交于B,C两点.
①当∠BAC=90°时.求抛物线G2的表达式;
②若60°<∠BAC<120°,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com