
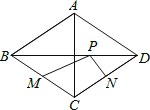
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是
【答案】5.
【解析】
试题分析:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
试题解析:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CP=![]() AC=3,BP=
AC=3,BP=![]() BD=4,
BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( ) ①a= ![]() ,b=
,b= ![]() ,c=
,c= ![]() ;
;
②a=6,∠A=45°;
③∠A=32°,∠B=58°;
④a=7,b=24,c=25.
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为( ) 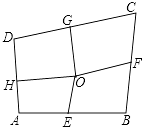
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的( )
A. 在同一平面内,若a∥b,b∥c,则a∥c
B. 在同一平面内,若a⊥b,b∥c,则a⊥c
C. 在同一平面内,若a⊥b,b⊥c,则a⊥c
D. 在同一平面内,若a⊥b,b⊥c,则a∥c
查看答案和解析>>
科目:初中数学 来源: 题型:
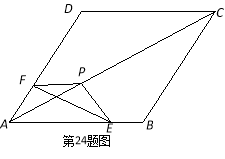
【题目】
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
⑴求∠EPF的大小;
⑵若AP=8,求AE+AF的值;
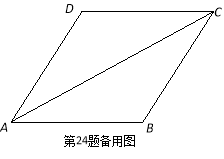
⑶若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F= . 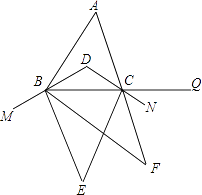
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C,B重合),点E为射线CA上一点,∠ADE=∠AED,设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= , β= .
②若∠BAC=54°,∠DAE=36°,则α= , β= .
③写出α与β的数量关系,并说明理由;
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.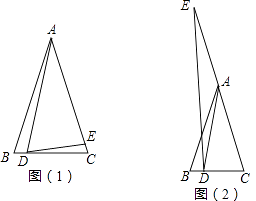
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动. 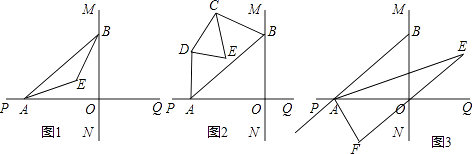
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com