
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C,B重合),点E为射线CA上一点,∠ADE=∠AED,设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= , β= .
②若∠BAC=54°,∠DAE=36°,则α= , β= .
③写出α与β的数量关系,并说明理由;
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.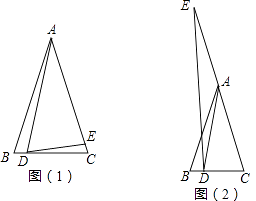
【答案】
(1)12°;6°;18°;9°
(2)
解:α=2β﹣180°,理由是:
如图(2),设∠E=x°,则∠DAC=2x°,
∴∠BAC=∠BAD+∠DAC=α+2x°,
∴∠B=∠ACB= ![]() ,
,
∵∠ADC=∠B+∠BAD,
∴β﹣x°= ![]() +α,
+α,
∴α=2β﹣180°.
【解析】解:(1)①∵∠DAE=30°,
∴∠ADE+∠AED=150°,
∴∠ADE=∠AED=75°,
∵∠BAC=42°,
∴α=42°﹣30°=12°,
∴∠ACB=∠B= ![]() =69°,
=69°,
∵∠ADC=∠B+α,
∴75°+β=69°+12°,
β=6°;
所以答案是:12°,6°;
②∵∠DAE=36°,
∴∠ADE+∠AED=144°,
∴∠ADE=∠AED=72°,
∵∠BAC=54°,
∴α=54°﹣36°=18°,
∴∠ACB=∠B= ![]() =63°,
=63°,
∵∠ADC=∠B+α,
∴72°+β=63°+18°,
β=9°;
所以答案是:18°,9°;
③α=2β,理由是:
如图(1),设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB= ![]() ,
,
∵∠ADE=∠AED,
∴∠AED= ![]() ,
,
∴β+∠ADE=α+∠ABC,
β+ ![]() =α+
=α+ ![]() ,
,
∴α=2β;
【考点精析】通过灵活运用三角形的“三线”,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内即可以解答此题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样的价格出售某种商品,“五一节”期间,两家商场都开展让利酬宾活动,其中甲商场打8折出售,乙商场对一次性购买商品总价超过300元后的部分打7折.
(1)设商品原价为x元,某顾客计划购此商品的金额为y元,分别就两家商场让利方式求出y关于x的函数解析式,并写出x的取值范围,作出函数图象(不用列表);
(2)顾客选择哪家商场购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,∠B=90°,AB=8,DH=3,平移距离为4,求阴影部分的面积为( ) 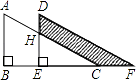
A.20
B.24
C.25
D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年我市财政计划安排社会保障和公共卫生等支出约1820000000元支持民生幸福工程,该数据用科学记数法表示为( )
A.18.2×108元
B.1.82×109元
C.1.82×1010元
D.0.182×1010元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解方程3x-3=2x-3时,小华同学是这样解的:
方程两边同加上3,得3x-3+3=2x-3+3.(1)
于是3x=2x.
方程两边同除以x,得3=2.(2)
所以此方程无解.
小华同学的解题过程是否正确?如果正确,请指出每一步的理由;如果不正确,请指出错在哪里,并加以改正.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com