练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算
    （1）（ ）2﹣（﹣3）0
    （2）8a3﹣3a5÷a2
    （3）4ab（2a2b2﹣ab+3）
    （4）（x+y）2﹣（x﹣y）（x+y）

    【答案】
    （1）解：原式= ﹣1=﹣
    （2）解：原式=8a3﹣3a3=5a3
    （3）解：原式=8a3b3﹣4a2b2+12ab
    （4）解：原式=（x2+2xy+y2）﹣（x2﹣y2）=2xy+2y2
    【解析】（1）根据零指数幂的意义即可求出答案．（2）根据同底数幂的除法即可求出答案．（3）根据单项式乘以多项式的法则即可求出答案．（4）根据完全平方公式以及平方差公式即可求出答案．
    【考点精析】利用零指数幂法则对题目进行判断即可得到答案，需要熟知零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一元二次方程(x－1)(x－2)＝0的两个根为x1，x2，且x1＞x2，则x1－2x2＝_______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（ ）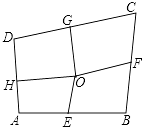
    A.6
    B.7
    C.8
    D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

    如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP=FP=6，EF=，∠BAD=60°，且AB＞．

    ⑴求∠EPF的大小；

    ⑵若AP=8，求AE+AF的值；

    ⑶若△EFP的三个顶点E，F，P分别在线段AB，AD，AC上运动，请直接写出AP长的最大值和最小值.

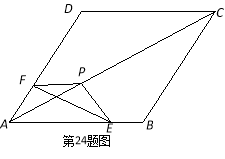
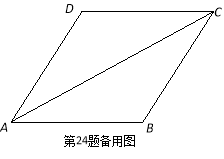
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=60°，BD、CD分别平分∠ABC、∠ACB，M、N、Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF分别平分∠EBC、∠ECQ，则∠F= ．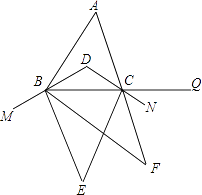

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，矩形ABCD中，AB=4cm，AD=2AB，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．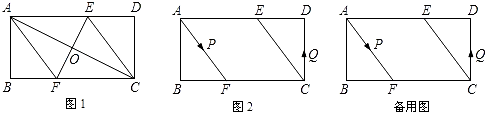

    （1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
    （2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
    ①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒．当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值；
    ②若点P、Q的速度分别为v1、v2（cm/s），点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，试探究a与b满足的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC中，∠ABC=∠ACB，D为线段CB上一点（不与C，B重合），点E为射线CA上一点，∠ADE=∠AED，设∠BAD=α，∠CDE=β．
    （1）如图（1），
    ①若∠BAC=42°，∠DAE=30°，则α= ， β= ．
    ②若∠BAC=54°，∠DAE=36°，则α= ， β= ．
    ③写出α与β的数量关系，并说明理由；
    （2）如图（2），当E点在CA的延长线上时，其它条件不变，请直接写出α与β的数量关系．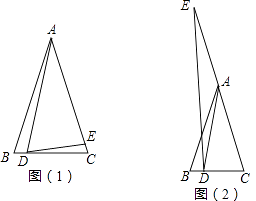

    查看答案和解析>>

    科目：初中数学 来源： 题型：

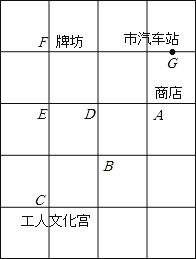
    【题目】 如图是某市区四个景点或单位（A为商店，C为工人文化宫，F为牌坊，G为市汽车站）的大致平面图．可将方格的边长看作是一个单位长度．

    （1）请你建立适当的直角坐标系，分别写出这四个地点的坐标．

    （2）在商店A处有游客甲和游客乙，甲按线路A→D→E→F步行到达牌坊；乙按A→B→C步行到达工人文化宫，若一个单位长度代表100米，你能比较一下两人哪个走的路程较多吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算的结果为a6的是（ ）
    A.a3+a3
    B.（a3）3
    C.a3a3
    D.a12÷a2

    查看答案和解析>>

    同步练习册答案