
����Ŀ��ij��ѧ�С����һ�λ�У���һ����ѧ����������̽����
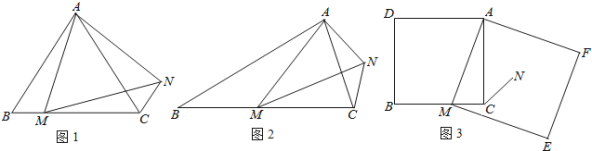
���ⷢ�֣���ͼ1���ڵȱ�������ABC�У���M�DZ�BC������һ�㣬����AM����AMΪ�����ȱ�������AMN������CN��֤����BM=CN��
��ʽ̽������ͼ2���ڵ���������ABC�У�BA=BC����ABC=��������MΪ��BC������һ�㣬��AMΪ��������������AMN��MA=MN��ʹ��AMN=��ABC������CN�������![]() ��ֵ�����ú�����ʽ�ӱ�ʾ������
��ֵ�����ú�����ʽ�ӱ�ʾ������
������⣺��ͼ3����������ADBC�У���MΪ��BC��һ�㣬��AMΪ������������AMEF��NΪ������AMEF�����ģ�����CN����������AMEF�ı߳�Ϊ![]() ��CN=
��CN=![]() ��������������ADBC�ı߳���
��������������ADBC�ı߳���
���𰸡����ⷢ�֣�֤������������ʽ̽����2sin![]() ��������⣺3
��������⣺3
��������
������������ⷢ�֣�������ABC����AMNΪ�ȱ������Σ��õ�AB=AC��AM=AN����BAC=��MAN=60���Ӷ��õ���BAC����CAM=��MAN����CAM������BAM=��CAN��֤����BAM�ա�CAN�����ɵõ�BM=CN��
��ʽ̽����������ABC����AMNΪ���������Σ��õ�![]() =1����ABC=��AMN��֤����ABC����AMN���õ�
=1����ABC=��AMN��֤����ABC����AMN���õ�![]() �����õ��������ε�����BA=BC���õ�
�����õ��������ε�����BA=BC���õ�![]() ��
��![]() ��֤����ABM����ACN���õ�
��֤����ABM����ACN���õ�![]() ����BD��AC����ͼ2������AB=BC���õ���ABD=
����BD��AC����ͼ2������AB=BC���õ���ABD=![]() ������sin��ABD=
������sin��ABD=![]() ���õ�AD=ABsin
���õ�AD=ABsin![]() ����AC=2AD=2ABsin
����AC=2AD=2ABsin![]() ���Ӷ��õ�
���Ӷ��õ�![]() =2sin
=2sin![]() ��
��
������⣺�����ı���ADBC��AMEFΪ�����Σ��õ���ABC=��BAC=45����MAN=45��������BAM=��CAN����![]() ���õ�
���õ�![]() ��֤����ABM����ACN���õ�
��֤����ABM����ACN���õ�![]() �������õ�
�������õ�![]() =cos45��=
=cos45��=![]() �����BM=2����AC=x�����ù��ɶ�������Rt��AMC��AC2+CM2=AM2����x2+��x��2��2=10����ã�x1=3��x2=��1����ȥ�������ɽ��
�����BM=2����AC=x�����ù��ɶ�������Rt��AMC��AC2+CM2=AM2����x2+��x��2��2=10����ã�x1=3��x2=��1����ȥ�������ɽ��
�⣺���ⷢ�֣�
�ߡ�ABC����AMNΪ�ȱ������Σ�
��AB=AC��AM=AN����BAC=��MAN=60��
���BAC����CAM=��MAN����CAM��
���BAM=��CAN��
����BAM����CAN��
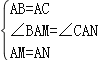 ��
��
���BAM�ա�CAN��
��BM=CN��
��ʽ̽������![]() =1����ABC=��AMN��
=1����ABC=��AMN��
���ABC����AMN��
��![]() ��
��
��AB=BC��
��![]() ��
��
��AM=MN
��![]() ��
��
���BAM=��CAN��
���ABM����ACN��
��![]() ��
��
��BD��AC����ͼ2��

��AB=BC��
���ABD=![]() ��
��
��sin��ABD=![]() ��
��
��AD=ABsin![]()
��AC=2AD=2ABsin![]() ��
��
��![]() =2sin
=2sin![]()
������⣺
��ͼ3������AB��AN��
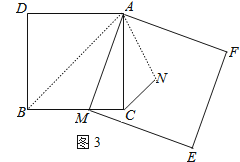
���ı���ADBC��AMEFΪ�����Σ�
���ABC=��BAC=45����MAN=45����
���BAC����MAC=��MAN����MAC
����BAM=��CAN��
��![]() ��
��
��![]() ��
��
���ABM����ACN��
��![]()
��![]() =cos45��=
=cos45��=![]() ��
��
��![]()
��BM=2��
��AC=x��
��Rt��AMC��
AC2+CM2=AM2
��x2+��x��2��2=10��
��ã�x1=3��x2=��1����ȥ����
�𣺱߳�Ϊ3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͷ������һ���ִ���װ�ػ��װ���������ʱ��y��h����װ���ٶ�x��t/h��֮��ĺ�����ϵ��ͼ��

��1����������������Ƕ��٣�д��y��x֮��ĺ�������ʽ��
��2������12��00�ִ�����Ŀ�ĵغӵ�������Ԥ��������8��00�ۿڽ��ܵ�̨��Ӱ�����ֹͣж����Ϊȷ���������ﰲȫж���������8t/h���ٶ�ж������ô��̨�絽��֮ǰ�ܷ�ж�������������Ҫ��̨�絽��ǰж������������ôÿСʱ����Ҫж���ٶֵĻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y1=k1x+b��k1Ϊ��������k1��0����ͼ���뷴��������y2=![]() ��k2Ϊ��������k2��0����ͼ���ཻ��A��1��2����B��m����1�����㣮
��k2Ϊ��������k2��0����ͼ���ཻ��A��1��2����B��m����1�����㣮

��1����һ�κ����ͷ����������Ľ���ʽ��
��2����A1��m1��n1����A��m2��n2����A3��m3��n3��Ϊ����������ͼ���ϵ����㣬��m1��m2��0��m3����ֱ��д��n1��n2��n3�Ĵ�С��ϵʽ��
��3�����ͼ����ֱ��д������x�IJ���ʽk1x+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��2016�½�����������ŵ�6�⣩ijС��ͬѧ��һ���ڲμӼ����Ͷ�ʱ����������������ʾ��
�Ͷ�ʱ�䣨Сʱ�� | 2 | 3 | 4 |
���� | 3 | 2 | 1 |
���й��ڡ��Ͷ�ʱ�䡱��������������ȷ���ǣ� ��
A����λ����2 B��������2 C��ƽ������3 D��������0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��ֱ��L��y=m��x+10����x�Ḻ���ᡢy��������ֱ���A��B���㣮

��1����OA=OBʱ����ȷ��ֱ��L�Ľ���ʽ��
��2���ڣ�1���������£���ͼ����ʾ����QΪAB�ӳ�����һ�㣬��ֱ��OQ����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM=8��BN=6����MN�ij���
��3����mȡ��ͬ��ֵʱ����B��y�����������˶����ֱ���OB��ABΪ�ߣ���BΪֱ�Ƕ����ڵ�һ����������������ֱ����OBF�͵���ֱ����ABE����EF��y����P�㣬��ͼ�ۣ�
�ʣ�����B��y�����������˶�ʱ���Բ���PB�ij��Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���½�ʦ��Ƹ�У���λ��ί���������������õ�һ��������ȥ��һ����߷ֺ�һ����ͷ֣��õ�һ����������ô�������������ͳ�����У�һ����ȵ��ǣ� ��
A.���
B.����
C.����
D.ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ����( )
A. -12-8=-4 B. -5+4=-9 C. -1-9=-10 D. -32=9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������뷨��2.098176ȡ����ֵ��������ȷ���ǣ� ��
A. 2.09����ȷ��0.01�� B. 2.098����ȷ��ǧ��λ��
C. 2.0����ȷ��ʮ��λ�� D. 2.0981����ȷ��0.0001��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD��, ��B����A��30�������A����B����C����D�Ķ����ֱ��� ( )
A��95����85����95����85�� B��85����95����8 5����95��
C��105����75����105����75�� D��75����105����75����105��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com