
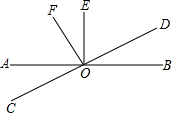
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.分析 (1)根据余角的定义即可得到结论;
(2)根据余角的定义,对顶角的性质即可得到结论;
(3)根据余角的定义,平角的定义即可得到结论.
解答 解:(1)∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∵∠AOC=∠BOD,
∴图中∠AOF的余角是∠AOC,∠EOF,∠BOD;
故答案为:∠AOC,∠EOF,∠BOD;
(2)① ∠AOC=∠EOF,②∠AOF=∠EOD,③∠EOC=∠BOF,④∠AOD=∠BOC;
∠AOC=∠EOF,②∠AOF=∠EOD,③∠EOC=∠BOF,④∠AOD=∠BOC;
故答案为:∠AOC=∠EOF,∠AOF=∠EOD,∠EOC=∠BOF,∠AOD=∠BOC
(3)互补,
∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∴∠AOC=∠EOF,
∵∠AOC=∠BOD,
∴∠BOD=∠EOF,
∴∠AOD+∠BOD=∠AOD+∠EOF=180°,
∴∠AOD=180°-α,
∴∠AOD与∠EOF互补.
点评 此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线,所求角与已知角的关系转化求解.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 160 | 150 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com