
【题目】如图,在![]() 中,
中,![]() 是边
是边![]() 上的中线,
上的中线,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线与
的平行线与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
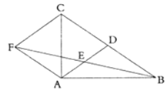
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() ,请写出图中所有与线段
,请写出图中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
【答案】(1)见解析;(2)CD、AD、CF、AF
【解析】
(1)根据平行线的性质求出∠BDE=∠FAE,根据全等三角形的判定定理推出AF=BD,再根据对边平行且相等的四边形是平行四边形即可证得;
(2)根据直角三角形斜边上的中线性质得出AD=CD=BD,得到四边形AFCD是菱形,根据菱形的性质得出CF=AF=CD=AD,即可得出答案.
∵AF∥BC,
∴∠BDE=∠FAE,
∵AD是BC边上的中线,E是AD的中点,
∴CD=BD,DE=AE,
在△BDE和△FAE中,
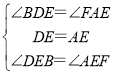 ,
,
∴△BDE≌△FAE(ASA),
∴AF=BD,
∵BD=CD,
∴AF=CD,
∵AF∥BC,
∴四边形CDAF为平行四边形;
(2)∵在△ABC中,∠BAC=90°,D为BC的中点,
∴AD=BD=CD,
∵四边形CDAF为平行四边形,AD=CD,
∴四边形CDAF为菱形,
∴AF=CF=CD=AD,
即BD=CD=AD=CF=AF,
图中所有与线段BD相等的线段有CD、AD、CF、AF.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
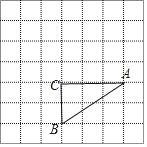
【题目】如图在7×7的正方形网格中,△ABC的顶点都在边长为1的小正方形的顶点上.
(1)将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A1BC1;
(2)求出旋转过程中,线段BA扫过的图形的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() .嘉嘉作
.嘉嘉作![]() ,
,![]() ,在正方形
,在正方形![]() 外,
外,![]() ,
,![]() 交于点
交于点![]() ;淇淇作
;淇淇作![]() ,
,![]() ,在正方形
,在正方形![]() 外,
外,![]() ,
,![]() 交于点
交于点![]() ,两人的作法中,能使四边形
,两人的作法中,能使四边形![]() 是正方形的是( )
是正方形的是( )
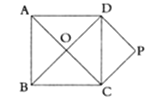
A.只有嘉嘉B.只有淇淇C.嘉嘉和淇淇D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(x﹣3)(x﹣5)=m(m>0)有两个实数根α,β(α<β),则下列选项正确的是( )
A. 3<α<β<5 B. 3<α<5<β C. α<2<β<5 D. α<3且β>5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交C于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
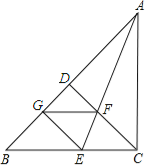
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1);四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2).则下列说法正确的是( )
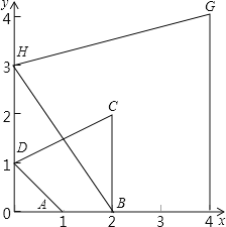
A.四边形ABCD与四边形BFGH相似但不位似
B.四边形ABCD与四边形BFGH位似但不相似
C.四边形ABCD与四边形BFGH位似,且位似比为l:![]()
D.四边形ABCD与四边形BFGH位似,且位似比为l:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.
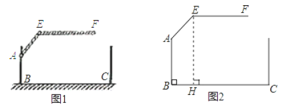
(1)求图2中点E到地面的高度(即EH的长.![]() ≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com