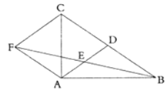
【题目】如图，在等边
中，点
为
上一点，
，
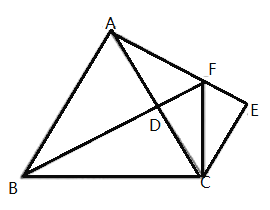
（1）求证：
≌
；
（2）延长
交
于
，连接
，若
，猜想线段
的数量关系，并证明你的猜想．
【答案】（1）见解析；（2）
，证明见解析
【解析】
（1）由题意利用等边三角形的性质以及全等三角形的判定进行分析求证即可；
（2）根据题意利用垂直平分线定理以及全等三角形性质求得△ABF是含30°角的直角三角形即可分析求证.
解：（1）∵△ABC是等边三角形 ，
∴BC=AC，∠BCD=60°，
∵
，
，
在△BCD和△ACE中，
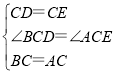
∴△BCD≌△ACE（SAS）.
（2）BF=2AF，
理由：∵AF=CF，AB=BC，
∴BF⊥AC且平分AC（垂直平分线定理），
∴BD为等边△ABC中AC边上的高，
∴BD平分∠ABC，
∴∠ABD=∠DBC=30°，
∵△BCD≌△ACE，
∴∠DBC=∠CAE，
∴∠ABD=∠CAE=30°，
∴∠BAF=∠BAC+∠CAE=90°，
∴在Rt△ABF中，BF=2AF．
科目：初中数学 来源： 题型：
【题目】已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F，如果BC边的长为10cm，AD的长为4cm，那么△ABC的周长为_____cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD中，∠A=140°，∠D=80°.
(1)如图1，若∠B=∠C，试求出∠C的度数；
(2)如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，对于一个图形，通过2种不同的方法计算它的面积时，可以得到一个数学等式．例如图①可以得到
，请解答下列问题：
（1）写出图②中所表示的等式： ；
（2）利用（1）中所得到的结论，解决下面的问题：已知
，
，求
的值；
（3）小明同学用2张边长为
的正方形纸片、3张边长为
的正方形纸片，5张边长分别为
的长方形纸片拼出了一个长方形，那么该长方形较长一边的长为多少？
（4）小明同学又用
张边长为的正方形纸片，
张边长为的正方形纸片、
张边长分别为
的长方形纸片拼出了一个面积为
的长方形，请问一共用掉多少张纸片？
查看答案和解析>>
科目：初中数学 来源： 题型：
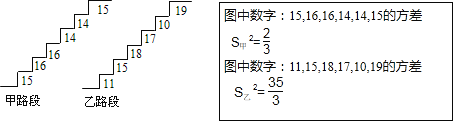
【题目】同学：你去过黄山吗？在黄山的上山路上，有一些断断续续的台阶，如图是其中的甲、乙段台阶路的示意图，图中的数字表示每一级台阶的高度（单位：cm）．
（1）两段台阶路有哪些相同点和不同点？
（2）哪段台阶路走起来更舒服，为什么？
（3）为方便游客行走，需要重新整修上山的小路．对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
是边
上的中线，
是的中点，过点
作的平行线与
的延长线相交于点
，连接
．
（1）求证：四边形
为平行四边形；
（2）若
，请写出图中所有与线段
相等的线段（线段除外）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用
，
表示直角三角形的两直角边（
），下列四个说法：
①
，②
，③
，④
.
其中说法正确的是 …………………………………………………………（ ）
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题8分）如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．
（1）求证：△ABC≌△AED；
（2）当∠B=140°时，求∠BAE的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
