
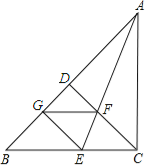
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交C于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
【答案】四边形GECF是菱形,理由详见解析.
【解析】
试题根据全等三角形的判定定理HL进行证明Rt△AEG≌Rt△AEC(HL),得到GE=EC;根据平行线EG∥CD的性质、∠BAC平分线的性质以及等量代换推知∠FEC=∠CFE,易证CF=CE;从而根据邻边相等的平行四边形是菱形进行判断.
试题解析:四边形GECF是菱形,理由如下:
∵∠ACB=90°,
∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,
∴GE=CE.
在Rt△AEG与Rt△AEC中,
![]() ,
,
∴Rt△AEG≌Rt△AEC(HL),
∴GE=EC,
∵CD是AB边上的高,
∴CD⊥AB,
又∵EG⊥AB,
∴EG∥CD,
∴∠CFE=∠GEA,
∵Rt△AEG≌Rt△AEC,
∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,
∴CE=CF,
∴GE=EC=FC,
又∵EG∥CD,即GE∥FC,
∴四边形GECF是菱形.



科目:初中数学 来源: 题型:
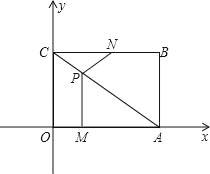
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)求P点的坐标(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
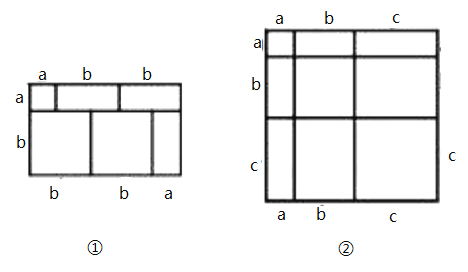
【题目】我们知道,对于一个图形,通过2种不同的方法计算它的面积时,可以得到一个数学等式.例如图①可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图②中所表示的等式: ;
(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学用2张边长为![]() 的正方形纸片、3张边长为
的正方形纸片、3张边长为![]() 的正方形纸片,5张边长分别为
的正方形纸片,5张边长分别为![]() 的长方形纸片拼出了一个长方形,那么该长方形较长一边的长为多少?
的长方形纸片拼出了一个长方形,那么该长方形较长一边的长为多少?
(4)小明同学又用![]() 张边长为
张边长为![]() 的正方形纸片,
的正方形纸片,![]() 张边长为
张边长为![]() 的正方形纸片、
的正方形纸片、![]() 张边长分别为
张边长分别为![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为![]() 的长方形,请问一共用掉多少张纸片?
的长方形,请问一共用掉多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是边
是边![]() 上的中线,
上的中线,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线与
的平行线与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
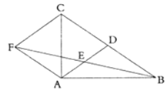
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若![]() ,请写出图中所有与线段
,请写出图中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
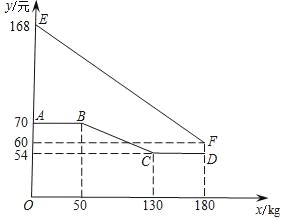
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A.B在反比例函数y=![]() 的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
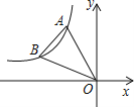
A.5B.-5C.4D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com