
 如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)
如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)分析 (1)由勾股定理计算出即可,
(2)作出辅助线,利用三角函数求解;
(3)由动点的特点表示出CQ=2t-5,BP=t-2,PC=7-t,再由面积公式计算即可;
(4)分情况讨论:点Q在BC上,在CD上,在BC上,第三种情况建立直角坐标系比较好.
解答 (1)解:∵DE⊥AB,
∴∠AED=90°,
在Rt△AED中,AD=$\sqrt{{AE}^{2}{+DE}^{2}}$=$\sqrt{{3}^{2}{+4}^{2}}$=5,
∵四边形ABCD是菱形,
∴AB=AD=5,
∴BE=AB-AE=5-3=2,
(2)解:如图1,当点P与点B重合时,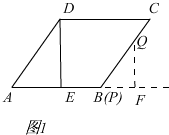
∵EB=2cm=t,
∴t=2s,BQ=2t=4cm,
∵四边形ABCD是菱形,
∴BC∥AD,
∴∠QBF=∠A,
过点Q作QF⊥AB交AB延长线于点F,
∴$\frac{QF}{BQ}$=$\frac{DE}{AD}$=SinA=$\frac{4}{5}$,
∴QF=$\frac{4}{5}$BQ=$\frac{4}{5}$×4=$\frac{16}{5}$,
(3)解:当2≤t≤2.5时,如图2,PQ=BQ-BP=2t-(t-2),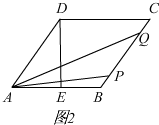
∴S=$\frac{1}{2}$[2t-(t-2)]×4=2t+4,
当2.5<t≤5时,如图3,CQ=2t-5,BP=t-2,PC=5-(t-2)=7-t,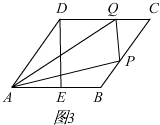
S=$\frac{1}{2}$(2t-5+5)×4-$\frac{1}{2}$×5×$\frac{4}{5}$(t-2)-$\frac{1}{2}$(2t-5)×$\frac{4}{5}$(7-t)=$\frac{4}{5}$t2-$\frac{28}{5}$t+18.
(4)解:点Q在线段BC上时,
∵△DEQ为等腰三角形,
①当DQ=DE时,连接DB,
由题意得,∠DBE=∠DBQ,DB=DB,
∴△DBE≌△DBQ,
∴BQ=BE=2,
∴t=2÷2=1,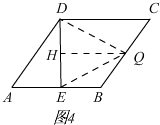
如图4,②当DQ=EQ时,作DH⊥DE,
∴DH=EH,
∴点H为DE中点,
∵QH∥AB,
∴BQ=$\frac{1}{2}$BC=$\frac{5}{2}$,
∴t=$\frac{5}{2}$÷2=$\frac{5}{4}$,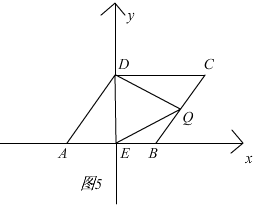
③当DE=QE时,以AB所在直线为x轴,以DE所在直线为x轴,点E为原点建立直角坐标系,如图5,
∴点D(0,4),E(0,0),B(2,0),C(5,4),
∴直线BC的解析式为y=$\frac{4}{3}$x-$\frac{8}{3}$,(m>2)
设Q(m,$\frac{4}{3}$m-$\frac{8}{3}$),
∴QB2=(m-2)2+($\frac{4}{3}$m-$\frac{8}{3}$)2=$\frac{25}{9}$(m-2)2=(2t)2,
∴m=$\frac{6}{5}$t+2或m=-$\frac{6}{5}$t+2(舍),
∴Q($\frac{6}{5}$t+2,$\frac{8}{5}$t),
∵DE=DQ=4,
∴QE2=($\frac{6}{5}$t+2)2+($\frac{8}{5}$t)2,
∴t=$\frac{-3-2\sqrt{21}}{5}$(舍)或t=$\frac{-3+2\sqrt{21}}{5}$.
点Q在CD上时,DQ=DE=4,
∵CD=5,
∴CQ=1,
∴t=(5+1)÷2=3
即:t=1或t=$\frac{5}{4}$或t=$\frac{-3+2\sqrt{21}}{5}$或t=3.
点评 此题是四边形的综合题,主要考查菱形的性质,三角形面积的计算以及等腰三角形的性质,解决本题的关键是用t表示线段和点的坐标,本题的难点是建立直角坐标系.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
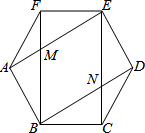 如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
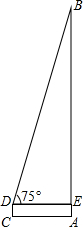 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com