
 阅读材料:
阅读材料:分析 (1)根据三角函数的公式,代入计算即可;
(2)根据仰角的概念、结合三角函数的公式、利用正切的定义计算.
解答 解:(1)
$\begin{array}{l}sin15°=sin(45°-30°)\\=sin45°cos30°-cos45°sin30°\\=\frac{{\sqrt{2}}}{2}•\frac{{\sqrt{3}}}{2}-\frac{{\sqrt{2}}}{2}•\frac{1}{2}\\=\frac{{\sqrt{6}-\sqrt{2}}}{4}\end{array}$
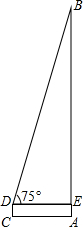
(2)在RT△BDE中,DE=AC=7,
∠BDE=75°,
tan∠BDE=$\frac{BE}{DE}$,
∴BE=DEtan∠BDE
=DEtan75°,
∵tan75°=tan(45°+30°)
$\begin{array}{l}=\frac{tan45°+tan30°}{1-tan45°tan30°}\\=\frac{{1+\frac{{\sqrt{3}}}{3}}}{{1-\frac{{\sqrt{3}}}{3}}}\\=\frac{{3+\sqrt{3}}}{{3-\sqrt{3}}}\\=2+\sqrt{3}\end{array}$
∴BE=7(2+$\sqrt{3}$)≈26.12,
∴信号塔AB的高度≈26.12+1.62≈27.7(米),
答:该信号塔AB的高度约为27.7米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确仰角俯角的概念、熟记锐角三角函数的定义、理解三角函数公式是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)
如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
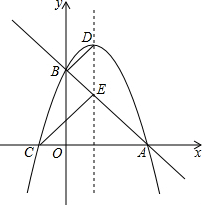 如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.
如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com