
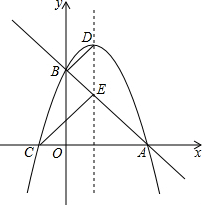
 如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.
如图,直线y=-x+3与x轴交于A点,与y轴交于B点,对称轴为x=1的抛物线经过A、B两点,与x轴的另一个交点为C,抛物线与对称轴交于D点,连接CE、CB、BD.分析 (1)根据自变量与函数值的对应关系,可得B、A点坐标,根据函数值相等的点关于对称轴对称,可得C点坐标,根据待定系数法,可得函数解析式;
(2)根据相似三角形的判断与性质,可得∠BDF=∠CEG,根据平行线的判定,可得答案;
(3)根据相似三角形的判定与性质,可得关于m的方程,根据解方程,可得m的值,根据自变量与函数值的对应关系,可得答案.
解答 解:(1)当x=0时,y=3,即B点(0,3),当y=0时,x=3,即A点坐标为(3,0),
由A、C关于x=1对称,得C(-1,0).
设抛物线的解析式为y=ax2+bx+c,将A、B、C坐标代入,得
$\left\{\begin{array}{l}{9a+3b+c=0}\\{a-b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=-x2+2x+3;
(2)证明:如图1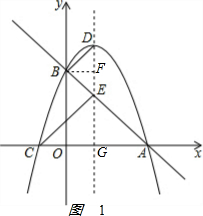 ,
,
作BF⊥DE于F,F点的坐标为(1,3),D(1,4),
BF=1,DF=4-3=1;
当x=1时,y=-1+3=2,即E点坐标为(1,2),G(1,0),
EG=2,CG=2.
$\frac{BF}{CG}$=$\frac{DF}{EG}$=$\frac{1}{2}$,∠BFD=∠CGE=90°,
∴△BFD∽△CGE,
∴∠BDF=∠CEG,
∴BD∥CE;
(3)设P点坐标为(m,-m+3),E(1,2),B(0,3),
由勾股定理,得
BE=$\sqrt{(0-1)^{2}+(3-2)^{2}}$=$\sqrt{2}$,CE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,PB=$\sqrt{{m}^{2}+(-m+3-3)^{2}}$=$\sqrt{2{m}^{2}}$,BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
①当△BDP∽△ECB,
$\frac{PB}{EB}$=$\frac{BD}{CE}$,即$\frac{\sqrt{2{m}^{2}}}{\sqrt{2}}$=$\frac{\sqrt{2}}{2\sqrt{2}}$,
解得m=±$\frac{1}{2}$,
即P1(-$\frac{1}{2}$,$\frac{7}{2}$),P2($\frac{1}{2}$,$\frac{5}{2}$),
②当△DBP∽△BEC时
$\frac{BP}{CE}$=$\frac{BD}{BE}$,即$\frac{\sqrt{2{m}^{2}}}{2\sqrt{2}}$=$\frac{\sqrt{2}}{\sqrt{2}}$
∴m2=4,m=±2
∴P3(2,1),P4(-2,5)
在直线AB上存在点P,使以B、D、P为顶点的三角形与△BCE相似,P1(-$\frac{1}{2}$,$\frac{7}{2}$),P2($\frac{1}{2}$,$\frac{5}{2}$),P3(2,1),P4(-2,5).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用相似三角形的判定与性质得出∠BDF=∠CEG是解题关键;利用相似三角形的对应边成比例得出关于m的方程是解题关键.


科目:初中数学 来源: 题型:解答题
 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.156×103 | B. | 0.1156×104 | C. | 1.156×105 | D. | 1.156×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
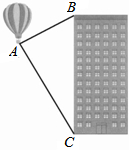 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )| A. | 80$\sqrt{3}$m | B. | 60$\sqrt{3}$m | C. | 40$\sqrt{3}$m | D. | 30$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com