
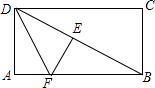
 如图,折叠矩形纸片ABCD,得折痕BD,再折叠使AD边与对角线BD重合,得折痕DF.若AB=4,BC=2,则AF=$\sqrt{5}$-1.
如图,折叠矩形纸片ABCD,得折痕BD,再折叠使AD边与对角线BD重合,得折痕DF.若AB=4,BC=2,则AF=$\sqrt{5}$-1. 分析 根据勾股定理可得BD=2$\sqrt{5}$,由折叠的性质可得△ADF≌△EDF,则ED=AD=2,EF=AF,则EB=2$\sqrt{5}$-2,在Rt△EBF中根据勾股定理求AF的即可.
解答 解:在Rt△ABD中,AB=4,AD=2,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
由折叠的性质可得,△ADF≌△EDF,
∴ED=AD=2,EF=AF,
∴EB=BD-ED=2$\sqrt{5}$-2,
设AF=x,则EF=AF=x,BF=4-x,
在Rt△EBF中,x2+(2$\sqrt{5}$-2)2=(4-x)2
解得x=$\sqrt{5}$-1,
即AF=$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1.
点评 此题主要考查了折叠的性质,综合利用了勾股定理的知识.认真分析图中各条线段的关系,也是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解全校同学对课程的喜欢情况,对某班男同学进行调查 | |
| B. | 了解某小区居民的防火意识,对你们班同学进行调查 | |
| C. | 了解商场的平均日营业额,选在周末进行调查 | |
| D. | 了解观众对所看电影的评价情况,对座号是奇数号的观众进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
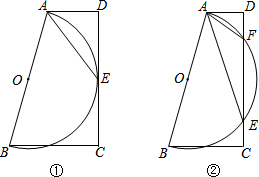 在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
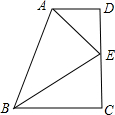 如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.
如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com