
����Ŀ��ij�е������Ŷ�һ�������õ�ʵ�������ݵ�����շѣ������շѱ����£�
��һ�������õ���������200�ȵIJ��ֵĵ��Ϊÿ��![]() Ԫ��
Ԫ��
�ڶ��������õ�������200�ȵ�������400�Ȳ��ֵĵ��Ϊÿ��![]() Ԫ��
Ԫ��
�����������õ�������400�ȵIJ��ֵĵ��Ϊÿ��![]() Ԫ��
Ԫ��
![]() ��֪С����ȥ��5�·ݵ��õ���Ϊ215�ȣ���С����5�·�Ӧ�����______Ԫ
��֪С����ȥ��5�·ݵ��õ���Ϊ215�ȣ���С����5�·�Ӧ�����______Ԫ![]()
![]() ��ȥ��6�·�С�����õ��ƽ�����Ϊ
��ȥ��6�·�С�����õ��ƽ�����Ϊ![]() Ԫ����С����ȥ��6�·ݵ��õ�����
Ԫ����С����ȥ��6�·ݵ��õ�����
![]() ��֪С����ȥ��7��8�·ݵ��õ�����700��
��֪С����ȥ��7��8�·ݵ��õ�����700��![]() �·ݵ��õ�������8�·ݵ��õ���
�·ݵ��õ�������8�·ݵ��õ���![]() �������µ��ܵ����384Ԫ����С����7��8�µ��õ����ֱ��Ƕ��٣�
�������µ��ܵ����384Ԫ����С����7��8�µ��õ����ֱ��Ƕ��٣�
���𰸡���1��109����2��С����ȥ��6�·ݵ��õ���Ϊ250�ȣ���3��С����ȥ��7�·ݵ��õ���Ϊ280�ȣ�8�·ݵ��õ���Ϊ420�ȣ�
��������
��1�������շѱ������ݵڶ������㼴�����С����5�·�Ӧ����ѣ�
��2�����ж�С�����õ������ڵڶ��������ݵڶ����շѱ��з�����⣻
��3����С����ȥ��7�·ݵ��õ���Ϊx�ȣ���8�·ݵ��õ���Ϊ��700��x���ȣ���x��200��200��x��300��300��x��350����������г�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��1��0.5��200+0.6����215��200��=109��Ԫ����
�ʴ�Ϊ��109��
��2����0.5+0.6����2=0.55��0.52������С�����õ糬��200�ȵ�������400�ȣ�
��С����ȥ��6�·ݵ��õ���Ϊa�ȣ�
��������ã�0.5��200+0.6����a��200��=0.52a����ã�a=250��
��С����ȥ��6�·ݵ��õ���Ϊ250�ȣ�
��3����������ȥ��7�·ݵ��õ���Ϊx�ȣ���8�·ݵ��õ���Ϊ��700��x���ȣ�������������ۣ�
�ٵ�x��200ʱ��700��x��500
��0.5x+0.5��200+0.6��200+0.8��700��x��400��=384����ã�x![]() ����ʱ700��x��500�ʲ��������⣻
����ʱ700��x��500�ʲ��������⣻
�ڵ�200��x��300ʱ����0.5��200��2+0.6��x��200��+200��0.6+0.8��700��x��400��=384����ã�x=280��700��280=420��
�۵�300��x��350ʱ����0.5��200��2+0.6����200��x��+0.6��700��x��200��=384�������⣮
��С����ȥ��7�·ݵ��õ���Ϊ280�ȣ�8�·ݵ��õ���Ϊ420�ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��BC��AC���ߵij��ֱ���![]() ��
��![]() ��
��![]() ��
��
��1����ABC��������� ����
��2������ͼ1��������ABC����ֱ��l�ԳƵ���A1B1C1��
��3������ͼ2�л�����DEF����DE��EF��DF���ߵij��ֱ���![]() ��
��![]() ��
��![]() �����ж���DEF����״��˵�����ɣ�
�����ж���DEF����״��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)���㣺(![]() ��
��![]() )2+(2
)2+(2![]() +
+![]() )(2
)(2![]() ��
��![]() )
)
(2)��ʽ�ֽ⣺9a2(x��y)+4b2(y��x)
(3)�Ȼ�������ֵ��![]() ��(a��1��
��(a��1��![]() )������a2��a��6=0��
)������a2��a��6=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ضԽ���AC���ۣ���B���ڵ�F����FC��AD��E��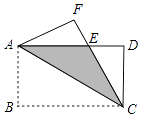
��1����֤����AFE�ա�CDE��
��2����AB=4��BC=8����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�����ĸ�������b��c���㣨b-3��2+|c+4|=0����a��b��c�ֱ��ǵ�A��B��C�������϶�Ӧ������
![]()
��1����A��ʾ����Ϊ______����B��ʾ����Ϊ______����C��ʾ����Ϊ______��
��2��������P��C�����������������˶�����P���ٶ���ÿ��2����λ���ȣ��˶������P����BΪ5����λ���ȣ�
��3������������һ��M��ʹ��M��A��B��C����ľ���֮�͵���13����д�����е�M��Ӧ��������д�������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ���2x2+kx��1=0��
��1����֤����������������ȵ�ʵ������
��2�������̵�һ�����ǩ�1������һ������kֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�����̻�����ij�ֵ��Ӳ�Ʒ�Ľ�����50Ԫ/���������г����з����ۼ���80Ԫ/��ʱ��ÿ�ܿ�����160���������۵���ÿ������2Ԫ����ÿ�ܿɶ�����20���������ۼ۸�ÿ������xԪ��xΪż������ÿ��������Ϊy����
��1��ֱ��д��������y���뽵��xԪ֮��ĺ�����ϵʽ��
��2�����̻�ÿ�ܻ�õ�����ΪWԪ�������۵��۶�Ϊ����Ԫʱ��ÿ���������������������Ƕ���Ԫ��
��3�����̻��ƻ�����������5200Ԫ������£�������Ҫ������Ԫ�����ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
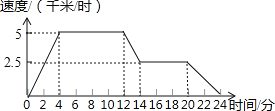
����Ŀ��ij���ѧ��С��ͽ���ؼң���ͼ��ʾ����ӳ�������ٶ���ʱ��ı仯��ϵ��
(1)�������ͼ����д�±���
ʱ��/�� | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
�ٶ�/(ǧ��/ʱ) |
(2)����ͼ��������������һ��С�����ߵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB�͡�COD��Ϊ����ֱ�������Σ���AOB=��COD=90�㣮����AD��BC����HΪBC�е㣬����OH��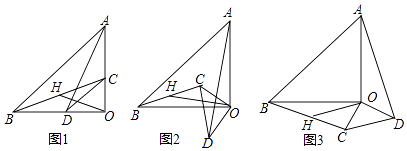
��1����ͼ1��ʾ����֤��OH= ![]() AD��OH��AD������֤����
AD��OH��AD������֤����
��2������COD�Ƶ�O��ת��ͼ2��ͼ3��ʾλ��ʱ���߶�OH��AD���������Ĺ�ϵ����ѡ��һ��ͼ��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com