
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.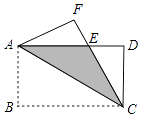
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
【答案】
(1)解:∵四边形ABCD是矩形,
∴AB=CD,∠B=∠D=90°,
∵将矩形ABCD沿对角线AC翻折,点B落在点F处,
∴∠F=∠B,AB=AF,
∴AF=CD,∠F=∠D,
在△AEF与△CDE中, 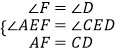 ,
,
∴△AFE≌△CDE;
(2)解:∵AB=4,BC=8,
∴CF=AD=8,AF=CD=AB=4,
∵△AFE≌△CDE,
∴AE=CE,EF=DE,
∴DE2+CD2=CE2,
即DE2+42=(8﹣DE)2,
∴DE=3,
∴EF=3,
∴图中阴影部分的面积=S△ACF﹣S△AEF= ![]() ×4×8﹣
×4×8﹣ ![]() ×4×3=10.
×4×3=10.
【解析】(1)由翻折性质可得∠F=∠B,AB=AF,再由矩形性质可得对边相等,可利用“角角边”证得全等;(2)阴影面积可转化为S△ACF﹣S△AEF,由 △AFE≌△CDE可知,面积可转化为求△CDE面积,须以DE为未知数由勾股定理建立方程,求出DE,进而求面积.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a= ![]() ;③ac=b﹣1;④
;③ac=b﹣1;④ ![]() >0
>0
其中正确的个数有( )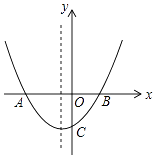
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市电力部门对一般照明用电实行“阶梯电价”收费,具体收费标准如下:
第一档:月用电量不超过200度的部分的电价为每度![]() 元.
元.
第二档:月用电量超过200度但不超过400度部分的电价为每度![]() 元.
元.
第三档:月用电量超过400度的部分的电价为每度![]() 元.
元.
![]() 已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元
已知小明家去年5月份的用电量为215度,则小明家5月份应交电费______元![]()
![]() 若去年6月份小明家用电的平均电价为
若去年6月份小明家用电的平均电价为![]() 元,求小明家去年6月份的用电量.
元,求小明家去年6月份的用电量.
![]() 已知小明家去年7、8月份的用电量共700度
已知小明家去年7、8月份的用电量共700度![]() 月份的用电量少于8月份的用电量
月份的用电量少于8月份的用电量![]() ,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
,两个月的总电价是384元,求小明家7、8月的用电量分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2020的坐标为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com