
【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a= ![]() ;③ac=b﹣1;④
;③ac=b﹣1;④ ![]() >0
>0
其中正确的个数有( )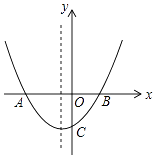
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:据图象可知a>0,c<0,b>0,
∴ ![]() <0,故④错误;
<0,故④错误;
∵OB=OC,
∴OB=﹣c,
∴点B坐标为(﹣c,0),
∴ac2﹣bc+c=0,
∴ac﹣b+1=0,
∴ac=b﹣1,故③正确;
∵A(﹣2,0),B(﹣c,0),抛物线线y=ax2+bx+c与x轴交于A(﹣2,0)和B(﹣c,0)两点,
∴2c= ![]() ,
,
∴2= ![]() ,
,
∴a= ![]() ,故②正确;
,故②正确;
∵ac﹣b+1=0,
∴b=ac+1,a= ![]() ,
,
∴b= ![]() c+1
c+1
∴2b﹣c=2,故①正确;
故答案为:C.
图像交y轴于负半轴,因此c<0,对称轴x=![]() <0,可知a、b同号,开口向上,a>0,因此b>0,
<0,可知a、b同号,开口向上,a>0,因此b>0, ![]() <0,故④错误;由OB=OC,得OB=﹣c,
<0,故④错误;由OB=OC,得OB=﹣c,
点B坐标为(﹣c,0),ac2﹣bc+c=0,c不等于0,同除以c,ac﹣b+1=0,故③正确;再把A(﹣2,0)代入解析式,得4a-2b+c=0,代换b=ac+1,可得4a-2ac-2+c=0,2a(2-c)+(c-2)=0,(c-2)(1-2a)=0,c-2不会等于0,因此a=![]() ,故②正确;把a=
,故②正确;把a=![]() 代入ac﹣b+1=0中,得2b﹣c=2,故①正确,故答案为:C.
代入ac﹣b+1=0中,得2b﹣c=2,故①正确,故答案为:C.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.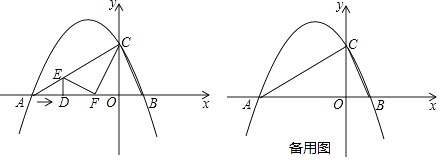
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣
﹣![]() )2+(2
)2+(2![]() +
+![]() )(2
)(2![]() ﹣
﹣![]() )
)
(2)因式分解:9a2(x﹣y)+4b2(y﹣x)
(3)先化简,再求值:![]() ÷(a﹣1﹣
÷(a﹣1﹣![]() ),其中a2﹣a﹣6=0.
),其中a2﹣a﹣6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2 ![]() ,点D为AC与反比例函数y=
,点D为AC与反比例函数y= ![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 .
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 . 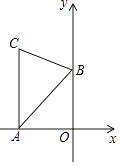
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.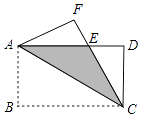
(1)求证:△AFE≌△CDE;
(2)若AB=4,BC=8,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB的长为10cm,点D是AB上的一个动点,不与点A重合,以AD为边作等边△ACD,过点D作DP⊥CD,过DP上一动点G(不与点D重合)作矩形CDGH,对角线交于点O,连接OA、OB,则线段OB的最小值是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com