
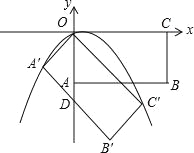
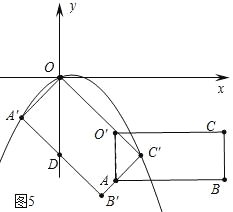
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨æÿ–ŒOABCµƒ∂•µ„OŒ™◊¯±Í‘≠µ„£¨∂•µ„A°¢Cµƒ◊¯±Í∑÷±Œ™£®0£¨©Å![]() £©°¢£®2
£©°¢£®2![]() £¨0£©£¨Ω´æÿ–ŒOABC»∆µ„OÀ≥ ±’Ζ˝◊™45°„µ√µΩæÿ–ŒOA°‰B°‰C°‰£¨±þA°‰B°‰”Îy÷·Ωª”⁄µ„D£¨æ≠π˝◊¯±Í‘≠µ„µƒ≈◊ŒÔœþy=ax2+bxÕ¨ ±æ≠π˝µ„A°‰°¢C°‰£Æ
£¨0£©£¨Ω´æÿ–ŒOABC»∆µ„OÀ≥ ±’Ζ˝◊™45°„µ√µΩæÿ–ŒOA°‰B°‰C°‰£¨±þA°‰B°‰”Îy÷·Ωª”⁄µ„D£¨æ≠π˝◊¯±Í‘≠µ„µƒ≈◊ŒÔœþy=ax2+bxÕ¨ ±æ≠π˝µ„A°‰°¢C°‰£Æ
£®1£©«Û≈◊ŒÔœþÀ˘∂‘”¶µƒ∫Ø ˝±Ì¥Ô Ω£ª
£®2£©–¥≥ˆµ„B°‰µƒ◊¯±Í£ª
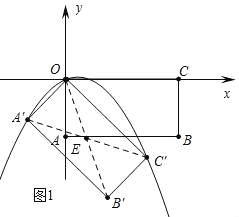
£®3£©µ„P «±þOC°‰…œ“ªµ„£¨π˝µ„P◊˜PQ°ÕOC°‰£¨Ωª≈◊ŒÔœþŒª”⁄y÷·”“≤ý≤ø∑÷”⁄µ„Q£¨¡¨Ω”OQ°¢DQ£¨…Ë°˜ODQµƒ√ʪ˝Œ™S£¨µ±÷±œþPQΩ´æÿ–ŒOA°‰B°‰C°‰µƒ√ʪ˝∑÷Œ™1£∫3µƒ¡Ω≤ø∑÷ ±£¨«ÛSµƒ÷µ£ª
£®4£©±£≥÷æÿ–ŒOA°‰B°‰C°‰≤ª∂Ø£¨Ω´æÿ–ŒOABC—ÿ…‰œþCO∑ΩœÚ“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»∆Ω“∆£¨…Ë∆Ω“∆ ±º‰Œ™t√Σ®t£æ0£©£Æµ±æÿ–ŒOABC”Îæÿ–ŒOA°‰B°‰C°‰÷ÿµ˛≤ø∑÷Õº–ŒŒ™÷·∂‘≥∆∂ý±þ–Œ ±£¨÷±Ω”–¥≥ˆtµƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=©Å![]() x2+
x2+![]() x£ª
x£ª
£®2£©B°‰£®1£¨©Å3£©£ª
£®3£©S°˜ODQ°‰=![]() °¡2°¡
°¡2°¡![]() =
=![]() £Æ
£Æ
£®4£©0°Ðt![]() ©Å2ªÚt=
©Å2ªÚt=![]() ªÚ2
ªÚ2![]() ©Å1°Ðt°Ð2
©Å1°Ðt°Ð2![]() ±£¨æÿ–ŒOABC”Îæÿ–ŒOA°‰B°‰C°‰÷ÿµ˛≤ø∑÷Õº–ŒŒ™÷·∂‘≥∆∂ý±þ–Œ£Æ
±£¨æÿ–ŒOABC”Îæÿ–ŒOA°‰B°‰C°‰÷ÿµ˛≤ø∑÷Õº–ŒŒ™÷·∂‘≥∆∂ý±þ–Œ£Æ
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©«Û≥ˆA°¢C¡Ωµ„◊¯±Í£¨∞—A°¢C¡Ωµ„◊¯±Í¥˙»Îy=ax2+bxΩ‚∑Ω≥Ã◊Ⱥ¥ø…£Æ
£®2£©»ÁÕº1÷–£¨¡¨Ω”A°‰C°‰£¨OB°‰Ωª”⁄µ„E£Æ«Û≥ˆµ„E◊¯±Í£¨∏˘æð÷–µ„◊¯±Íπ´ Ωº¥ø…Ω‚æˆŒ £Æ
£®3£©∑÷¡Ω÷÷«È–Œ¢Ÿµ±OP£∫PC°‰=1£∫3 ±£¨P£®![]() £¨©Å
£¨©Å![]() £©£¨«Û≥ˆ÷±œþPQµƒΩ‚Œˆ Ω£¨¿˚”√∑Ω≥Ã◊È«Û≥ˆµ„Q◊¯±Íº¥ø…£Æ¢⁄µ±OP°‰£∫P°‰C°‰=3£∫1 ±£¨P°‰£®
£©£¨«Û≥ˆ÷±œþPQµƒΩ‚Œˆ Ω£¨¿˚”√∑Ω≥Ã◊È«Û≥ˆµ„Q◊¯±Íº¥ø…£Æ¢⁄µ±OP°‰£∫P°‰C°‰=3£∫1 ±£¨P°‰£®![]() £¨©Å
£¨©Å![]() £©£¨∑Ω∑®¿ýÀ∆£Æ
£©£¨∑Ω∑®¿ýÀ∆£Æ
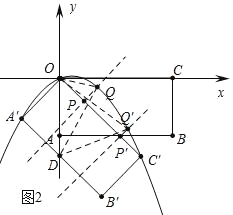
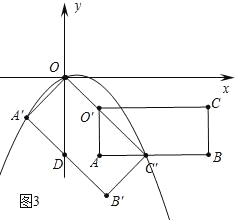
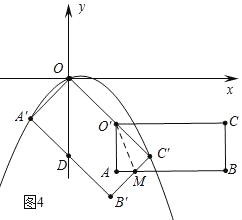
£®4£©∑÷±«Û≥ˆ¢Ÿ»ÁÕº3÷–£¨µ±ABæ≠π˝µ„C°‰ ±£¨¢⁄»ÁÕº4÷–£¨µ±O°‰C°‰=O°‰A=![]() ±£¨¢€»ÁÕº5÷–£¨µ±µ„A‘⁄÷±œþB°‰C°‰…œ ±µƒ ±º‰t£¨π€≤ÏÕºœÛº¥ø…Ω‚æˆŒ £Æ
±£¨¢€»ÁÕº5÷–£¨µ±µ„A‘⁄÷±œþB°‰C°‰…œ ±µƒ ±º‰t£¨π€≤ÏÕºœÛº¥ø…Ω‚æˆŒ £Æ
‘Ã‚Ω‚Œˆ£∫£®1£©»ÁÕº1÷–£¨
”…“‚A°‰£®©Å1£¨©Å1£©£¨C°‰£®2£¨©Å2£©£¨∞—A°‰£®©Å1£¨©Å1£©£¨C°‰£®2£¨©Å2£©¥˙»Îy=ax2+bxµ√![]() £¨
£¨
Ω‚µ√ £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=©Å![]() x2+
x2+![]() x£Æ
x£Æ
£®2£©»ÁÕº1÷–£¨¡¨Ω”A°‰C°‰£¨OB°‰Ωª”⁄µ„E£Æ°þÀƒ±þ–ŒOA°‰B°‰C°‰ «æÿ–Œ£¨
°ýA°‰E=EC°‰£¨OE=EB°‰£¨°þA°‰£®©Å1£¨©Å1£©£¨C°‰£®2£¨©Å2£©£¨°ýE£®![]() £¨©Å
£¨©Å![]() £©£¨°ýB°‰£®1£¨©Å3£©£Æ
£©£¨°ýB°‰£®1£¨©Å3£©£Æ
£®3£©»ÁÕº2÷–£¨°þ÷±œþPQΩ´æÿ–ŒOA°‰B°‰C°‰µƒ√ʪ˝∑÷Œ™1£∫3µƒ¡Ω≤ø∑÷£¨
°ýOP£∫PC°‰=1£∫3ªÚOP°‰£∫P°‰C°‰=3£∫1£Æ
¢Ÿµ±OP£∫PC°‰=1£∫3 ±£¨P£®![]() £¨©Å
£¨©Å![]() £©£¨÷±œþPQµƒΩ‚Œˆ ΩŒ™y=x©Å1£¨
£©£¨÷±œþPQµƒΩ‚Œˆ ΩŒ™y=x©Å1£¨
”…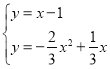 £¨Ω‚µ√
£¨Ω‚µ√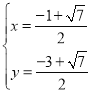 ªÚ
ªÚ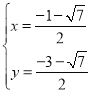 £¨°þµ„Q‘⁄µ⁄ÀƒœÛœÞ£¨
£¨°þµ„Q‘⁄µ⁄ÀƒœÛœÞ£¨
°ýQ£®![]() £¨
£¨![]() £©£Æ°þD£®0£¨©Å2£©£¨°ýS°˜ODQ=
£©£Æ°þD£®0£¨©Å2£©£¨°ýS°˜ODQ=![]() °¡2°¡
°¡2°¡![]() =
=![]() £Æ
£Æ
¢⁄µ±OP°‰£∫P°‰C°‰=3£∫1 ±£¨P°‰£®![]() £¨©Å
£¨©Å![]() £©£¨°ý÷±œþP°‰Q°‰µƒΩ‚Œˆ ΩŒ™y=x©Å3£¨
£©£¨°ý÷±œþP°‰Q°‰µƒΩ‚Œˆ ΩŒ™y=x©Å3£¨
”…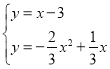 Ω‚µ√
Ω‚µ√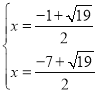 ªÚ
ªÚ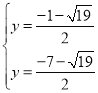 £¨
£¨
°ýQ°‰£®![]() £¨
£¨![]() £©£¨°ýS°˜ODQ°‰=
£©£¨°ýS°˜ODQ°‰=![]() °¡2°¡
°¡2°¡![]() =
=![]() £Æ
£Æ
£®4£©»ÁÕº3÷–£¨µ±ABæ≠π˝µ„C°‰ ±£¨t=2![]() ©Å2£¨
©Å2£¨
»ÁÕº4÷–£¨µ±O°‰C°‰=O°‰A=![]() ±£¨AB”ÎB°‰C°‰Ωª”⁄µ„M£¨¡¨Ω”O°‰M£¨‘Ú°˜O°‰MA°’°˜O°‰MC°‰£¨
±£¨AB”ÎB°‰C°‰Ωª”⁄µ„M£¨¡¨Ω”O°‰M£¨‘Ú°˜O°‰MA°’°˜O°‰MC°‰£¨
¥À ±t=OO°‰=2![]() ©Å
©Å![]() =
=![]() £¨
£¨
»ÁÕº5÷–£¨µ±µ„A‘⁄÷±œþB°‰C°‰ ±…œ£¨t=OO°‰=2![]() ©Å1£Æ
©Å1£Æ
◊€…œÀ˘ ˆ£¨π€≤ÏÕº–Œø…÷™0°Ðt![]() ©Å2ªÚt=
©Å2ªÚt=![]() ªÚ2
ªÚ2![]() ©Å1°Ðt°Ð2
©Å1°Ðt°Ð2![]() ±£¨æÿ–ŒOABC”Îæÿ–ŒOA°‰B°‰C°‰÷ÿµ˛≤ø∑÷Õº–ŒŒ™÷·∂‘≥∆∂ý±þ–Œ£Æ
±£¨æÿ–ŒOABC”Îæÿ–ŒOA°‰B°‰C°‰÷ÿµ˛≤ø∑÷Õº–ŒŒ™÷·∂‘≥∆∂ý±þ–Œ£Æ


 ”Æ‘⁄øŒÃ√√˚ ¶øŒ ±º∆ªÆœµ¡–¥∞∏
”Æ‘⁄øŒÃ√√˚ ¶øŒ ±º∆ªÆœµ¡–¥∞∏ ÃÏÃϜڅœøŒ ±Õ¨≤Ω—µ¡∑œµ¡–¥∞∏
ÃÏÃϜڅœøŒ ±Õ¨≤Ω—µ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2017ƒÍ4‘¬6»’£¨ΩªÕ®‘À ‰≤øø∆—ß—–æø‘∫∂‘Õ‚∑¢≤º°∂2017ƒÍµ⁄“ªºæ∂»÷–π˙÷˜“™≥« –∆Ô––±®∏Ê°∑£¨±®∏Êœ‘ 棨‘⁄≥µæ˘ π”√¥Œ ˝∑Ω√Ê£¨¿•√˜≈≈√˚µ⁄“ª£¨≥…Œ™°∞◊Ó∞Æ∆Ôπ≤œÌµ•≥µµƒ≥« –°±£Æƒø«∞“—æ≠Õ∂»Î¿•√˜µƒπ≤œÌµ•≥µ‘º”–112000¡æ£ÆΩ´°∞112000°±”√ø∆—ߺ« ˝∑®±Ì 挙£® £©
A.1.12°¡103
B.1.12°¡104
C.1.12°¡105
D.11.2°¡104
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ùy=x+2©Åb «’˝±»¿˝∫Ø ˝£¨‘Úbµƒ÷µ «£®°°°°£©
A. 0 B. ©Å2 C. 2 D. ©Å0.5
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº∆À„£∫£®©Å3£©°¡2µƒΩ·π˚ «£®°°°°£©
A.©Å6B.6C.©Å1D.9
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫”ƒœπ√ƒÔ÷ÏÊ√ «“ªŒª∑«≥£”≈–„∫Õ±ªπ€÷⁄œ≤∞Ƶƒ≈≈«Ú‘À∂Ø‘±£¨œ¬√Ê“ª◊È ˝æð «À˝‘⁄ƒ≥œµ¡–»¸÷–µƒµ√∑÷Õ≥º∆£®µ•Œª£∫∑÷£©£∫20£¨21£¨24£¨27£¨19£¨23£¨24£¨26£¨23£¨24£¨‘Ú¥Àœµ¡–»¸µ√∑÷µƒ÷⁄ ˝∫Õ÷–Œª ˝∑÷± « £® £©
A.23£¨24B.23£¨23.5C.24£¨23D.24£¨23.5
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨–°√˜Ω´“ª∏ˆ’˝∑Ω–Œ÷ΩºÙ≥ˆ“ª∏ˆøÌŒ™4cmµƒ≥§Ãı∫Û£¨‘Ÿ¥” £œ¬µƒ≥§∑Ω–Œ÷Ω∆¨…œºÙ»•“ª∏ˆøÌŒ™5cmµƒ≥§Ãı£¨»Áπ˚¡Ω¥ŒºÙœ¬µƒ≥§Ãı√ʪ˝’˝∫√œýµ»£¨ƒ«√¥√ø“ª∏ˆ≥§Ãı√ʪ˝Œ™£® £© 
A.16cm2
B.20cm2
C.80cm2
D.160cm2
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨PŒ™∆Ω––Àƒ±þ–ŒABCD±þAD…œ“ªµ„£¨E°¢F∑÷±Œ™PB°¢PCµƒ÷–µ„£¨°˜PEF°¢°˜PDC°¢°˜PABµƒ√ʪ˝∑÷±Œ™S°¢S1°¢S2£¨»ÙS=2£¨‘ÚS1+S2=£® £©

A£Æ4 B£Æ6 C£Æ8 D£Æ≤ªƒÐ»∑∂®
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂ı÷ð –ªØπ§≤ƒ¡œæ≠œ˙π´Àæπ∫Ω¯“ª÷÷ªØπ§‘≠¡œ»Ù∏…«ßøÀ£¨º€∏ÒŒ™√ø«ßøÀ30‘™£ÆŒÔº€≤ø√≈πÊ∂®∆‰œ˙ €µ•º€≤ª∏þ”⁄√ø«ßøÀ60‘™£¨≤ªµÕ”⁄√ø«ßøÀ30‘™£Ææ≠ –≥°µ˜≤È∑¢œ÷£∫»’œ˙ €¡øy£®«ßøÀ£© «œ˙ €µ•º€x£®‘™£©µƒ“ª¥Œ∫Ø ˝£¨«“µ±x=60 ±£¨y=80£ªx=50 ±£¨y=100£Æ‘⁄œ˙ €π˝≥Ã÷–£¨√øÃϪπ“™÷ß∏∂∆‰À˚∑—”√450‘™£Æ
£®1£©«Û≥ˆy”Îxµƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆ◊‘±‰¡øxµƒ»°÷µ∑∂Œß£Æ
£®2£©«Û∏√π´Àæœ˙ €∏√‘≠¡œ»’ªÒ¿˚w£®‘™£©”Îœ˙ €µ•º€x£®‘™£©÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£Æ
£®3£©µ±œ˙ €µ•º€Œ™∂ý…Ÿ‘™ ±£¨∏√π´Àæ»’ªÒ¿˚◊Ó¥Û£ø◊Ó¥ÛªÒ¿˚ «∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com