Question

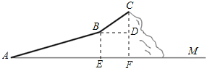
【题目】数学活动小组组织一次登山活动，他们从山脚下点出发沿斜坡到达点，再从点沿斜坡到达山顶点，路线如图所示．斜坡的长为米，斜坡的长为米，坡度是，已知点海拔米，点海拔米．

问点测得点的俯角为________，并求点的海拔；

求斜坡的坡度；

为了方便上下山，若在到之间架设一条钢缆，求钢缆的长度．

Answer 1

【答案】（1）45°，米；（2）坡度为；（3）米.

【解析】

（1）过C作CF⊥AM，F为垂足，过B点作BE⊥AM，BD⊥CF，E、D为垂足，根据斜坡BC的坡度是1：1，可得∠CBD=45°，继而可求得CD的长度，求出B点的高度；
（2）根据（1）中求得B点的高度，AB=200米，利用勾股定理求出AE的长度，易求得AB的坡度；
（3）根据CF⊥AM，BE⊥AM，BD⊥CF，得出四边形EFDB是矩形，继而可求得AF=800米，CF=600米，利用勾股定理即可求得AC的长度．

如图，过作，为垂足，过点作，，、为垂足，

∵斜坡的坡度是，

∴，

∴，

∴

∴在点测得点的俯角为，

∴，又米，

∴（米），

∵点海拔米，点海拔米，

∴（米）

∴点的铅直高度为（米），

即斜坡点处的高度为米；

∵米，

∴米，（米），

∴的坡度，

故斜坡的坡度为．

∵，，，

∴四边形是矩形，

∴米，米，

∴米，米，

∴米．

即钢缆的长度为米．