
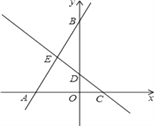
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=��x+b�������ύ��C��D���㣬ֱ��AB�������ύ��A��B���㣬�߶�OA��OC�ij��Ƿ���x2��3x+2=0����������OA��OC����
��1�����A��C�����ꣻ
��2��ֱ��AB��ֱ��CD���ڵ�E������E���߶�AB���е㣬����������y=![]() ��k��0����ͼ���һ����֧������E����k��ֵ��
��k��0����ͼ���һ����֧������E����k��ֵ��
��3���ڣ�2���������£���M��ֱ��CD�ϣ�����ƽ�����Ƿ���ڵ�N��ʹ�Ե�B��E��M��NΪ������ı��������Σ������ڣ���ֱ��д�����������ĵ�N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A����2��0����C��1��0��;��2��k=��2;(3)���ڣ���N������Ϊ����![]() ��4+
��4+![]() ������
������![]() ��4��
��4��![]() ����
����![]() ��
��![]() ����
����
����������������1�����÷ֽ���ʽ����һԪ���η���x-3x+2=0���ɵó�OA��OC��ֵ���ٸ��ݵ����ڵ�λ�ü��ɵó�A��C�����ꣻ��2�����ݵ�C���������ô���ϵ�����������ֱ��CD�Ľ���ʽ�����ݵ�A��B�ĺ������ϵ�EΪ�߶�AB���е㼴�ɵó���E�ĺ����꣬�������ֱ��CD�Ľ���ʽ�м��������E�����꣬�����ô���ϵ�����������kֵ����3��������ڣ����M������Ϊ��m��-m+1�����ֱ���BEΪ�ߡ�BEΪ�Խ��������ǣ��������ε������ҳ�����m�ķ��̣��ⷽ�̼��ɵó���M�����꣬�ٽ�ϵ�B��E�����꼴�ɵó���N������.
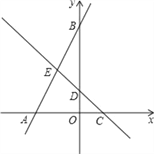
�����������1��x2��3x+2=(x��1)(x��2)=0��
��x1=1��x2=2��
��OA��OC��
��OA=2��OC=1��
��A����2��0����C��1��0����
��2����C��1��0������y=��x+b��
�ã�0=��1+b����ã�b=1��
��ֱ��CD�Ľ���ʽΪy=��x+1��
�ߵ�EΪ�߶�AB���е㣬A����2��0����B�ĺ�����Ϊ0��
���E�ĺ�����Ϊ��1��
�ߵ�EΪֱ��CD��һ�㣬
��E����1��2����
����E����1��2������y=![]() ��k��0����
��k��0����
�ã�2=![]() ����ã�k=��2��
����ã�k=��2��
3.������ڣ�
���M��������m����m+1����
�Ե�B��E��M��NΪ������ı��������η������������ͼ��ʾ����
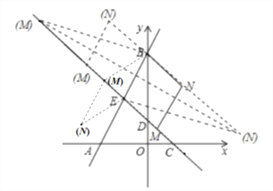
�����߶�BEΪ��ʱ����E����1��2����A����2��0����EΪ�߶�AB���е㣬
��B��0��4����
��BE=![]() AB=
AB=![]()
![]() ��
��
���ı���BEMNΪ���Σ�
��EM=![]()
![]() =BE=
=BE=![]() ��
��
��ã�m1=![]() ��m2=
��m2=![]()
��M��![]() ��2+
��2+![]() ����
����![]() ��2��
��2��![]() ����
����
��B��0��4����E����1��2����
��N����![]() ��4+
��4+![]() ����
����![]() ��4��
��4��![]() ����
����
�����߶�BEΪ�Խ���ʱ��MB=ME��
��![]() ��
��
��ã�m3=��![]() ��
��
��M����![]() ��
��![]() ����
����
��B��0��4����E����1��2����
��N��0��1+![]() ��4+2��
��4+2��![]() ��������
��������![]() ��
��![]() ����
����
���Ͽɵã�����ƽ���ڴ��ڵ�N��ʹ�Ե�B��E��M��NΪ������ı��������Σ���N������Ϊ����![]() ��4+
��4+![]() ������
������![]() ��4��
��4��![]() ������
������![]() ��
��![]() ����
����


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
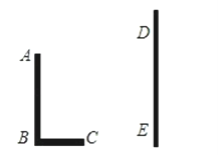
����Ŀ����֪����ͼ��AB��DE��ֱ���ڵ����ϵ�����������AB=7m��ijһʱ��AB��̫�����µ�ͶӰBC=4m��
��1��������ͼ�л�����ʱDE�������µ�ͶӰ��
��2���ڲ���AB��ͶӰʱ��ͬʱ������DE�������µ�ͶӰ��Ϊ8m������DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() ��
��![]() ��
��
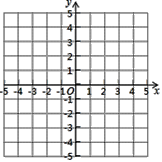
![]() ��һ�κ����ı���ʽ��
��һ�κ����ı���ʽ��
![]() ��P��x���ϣ���
��P��x���ϣ���![]() ��ֵ��Сʱ����ͼ�л�����P���������P�����꣮
��ֵ��Сʱ����ͼ�л�����P���������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�BD������һ���Խ��ߣ���A��C������AE��BD��CF��BD������ֱ�ΪE��F���ӳ�AE��CF�ֱ�CD��AB��M��N��
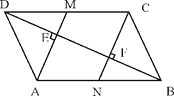
��1����֤���ı���CMAN��ƽ���ı��Ρ�
��2����֪DE��4��FN��3����BN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2016��Ϊ���á�����ƶ����Ͷ���ʽ�1200��Ԫ������ذ��ã����滮Ͷ����ذ����ʽ����ƽ���������������ڱ��ֲ��䣬��֪2018����2016��Ļ�����������Ͷ����ذ����ʽ�1500��Ԫ��
��1��2017��õ�Ͷ����ذ����ʽ�Ϊ����Ԫ��
��2����2017����ذ��õľ���ʵʩ�У��õ�Ҫ��Ͷ���������Ȱ�Ǩ�ⷿ�������ʽ���2017��õ�Ͷ����ذ����ʽ��25%���涨ǰ1000��������1000������ÿ��ÿ�콱��8Ԫ��1000���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬��2017��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ǶԽ���AC�ϵ����㣬��AE��CF.
(1)ͼ�����ļ���ȫ�������Σ���һһ�о٣�
(2)��֤��ED��BF.
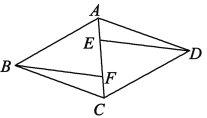
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ��������Σ�
���������![]() ��
��![]() ���ϵĸߣ�������
���ϵĸߣ�������![]() ��һ��
��һ��![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���֪
�ϣ���֪![]() ��
��![]() ��
��

��1����֤��![]() ��
��
��2�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ȤС�������ij������ĸ߶ȣ�������A�����ݶ�C������Ϊ30����Ȼ����AD����ǰ��10�ף�����B�㣬��B�����ݶ�C������Ϊ60������֪������AE�ĸ߶�Ϊ1�ף�����������ǵIJ������ݼ��㽨����CF�ĸ߶ȣ�����������ţ���
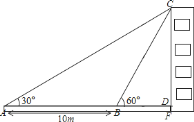
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�һ�κ���y=ax+c�Ͷ��κ���y=a��x+c��2��ͼ�����Ϊ��������
A.  B.
B. 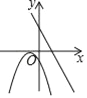 C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com