
【题目】已知ax=5,ax+y=30,求ax+ay的值.
科目:初中数学 来源: 题型:
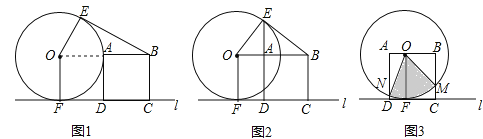
【题目】半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,⊙O与l相切于点F,DC在l上.
(1)过点B作的一条切线BE,E为切点.
①填空:如图1,当点A在⊙O上时,∠EBA的度数是 ;
②如图2,当E,A,D三点在同一直线上时,求线段OA的长;
(1)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC.与OF重合时结束移动,M,N分别是边BC,AD与⊙O的公共点,求扇形MON的面积的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.

(1)此变化过程中,__是自变量,__是因变量.
(2)甲的速度__乙的速度.(大于、等于、小于)
(3)6时表示__;
(4)路程为150km,甲行驶了__小时,乙行驶了__小时.
(5)9时甲在乙的__(前面、后面、相同位置)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各条件中,能作出唯一的△ABC的是( )
A. AB=4,BC=5,AC=10 B. AB=5,BC=4,∠A=40°
C. ∠A=90°,AB=10 D. ∠A=60°,∠B=50°,AB=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市因水而名,因水而美,因水而兴,市政府作出了“五水共治”决策:治污水、防洪水、排涝水、保供水、抓节水.某区某乡镇对某河道进行整治,由甲乙两工程队合作20天可完成.已知甲工程队单独整治需60天完成.
(1)求乙工程队单独完成河道整治需多少天?
(2)若甲乙两工程队合做a天后,再由甲工程队单独做 天(用含a的代数式表示)可完成河道整治任务.
(3)如果甲工程队每天施工费5000元,乙工程队每天施工费为1.5万元,先由甲乙两工程队合作整治,剩余工程由甲工程队单独完成,问要使支付两工程队费用最少,并且确保河道在40天内(含40天)整治完毕,问需支付两工程队费用最少多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
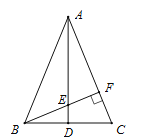
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班分两组志愿者去社区服务,第一组20人,第二组26人.现第一组发现人手不够,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A. 20=2(26﹣x) B. 20+x=2×26 C. 2(20+x)=26﹣x D. 20+x=2(26﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,BE=DF.
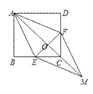
(1)求证:AE=AF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
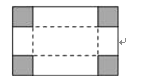
【题目】如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后(剩下的部分做成一个)容积为90立方米的无盖长方体箱子,已知长方体箱子底面积的长比宽多4米,求矩形铁皮的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com