
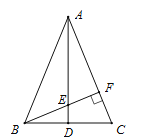
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.
科目:初中数学 来源: 题型:
【题目】一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
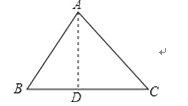
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm

(1)填空:AD= (cm),DC= (cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=![]() ,sin15°=
,sin15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点P (a,b)若规定以下两种变换:①f(a,b)=(﹣a,﹣b),如f(1,2)=(﹣1,﹣2);②g(a,b)=(b,a),如g(1,3)=(3,1)按照以上变换,那么f(g(a,b))等于( )
A. (﹣b,﹣a) B. (a,b) C. (b,a) D. (﹣a,﹣b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com