
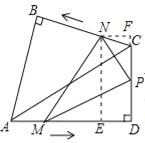
【题目】如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm

(1)填空:AD= (cm),DC= (cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=![]() ,sin15°=
,sin15°=![]() )
)
【答案】(1)![]() ;
;![]() ;
;
(2)![]() ;
;
(3)![]()
【解析】
试题分析:(1)由勾股定理求出AC,由∠CAD=30°,得出DC=![]() AC=
AC=![]() ,由三角函数求出AD即可;
,由三角函数求出AD即可;
(2)过N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,则NE=DF,求出∠NCF=75°,∠FNC=15°,由三角函数求出FC,得NE=DF=![]() x
x![]() ,即可得出结果;
,即可得出结果;
(3)由三角函数求出FN,得出PF,△PMN的面积y=梯形MDFN的面积﹣△PMD的面积﹣△PNF的面积,得出y是x的二次函数,即可得出y的最大值.
试题解析:(1)∵∠ABC=90°,AB=BC=4cm,
∴AC=![]() =
=![]() =
=![]() ,
,
∵∠ADC=90°,∠CAD=30°,
∴DC=![]() AC=
AC=![]() ,
,
∴AD=![]() DC=
DC=![]() ;
;
故答案为:![]() ;
;![]()
(2)过点N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,如图所示:
则NE=DF,
∵∠ABC=∠ADC=90°,AB=BC,∠CAD=30°,
∴∠ACB=45°,∠ACD=60°,
∴∠NCF=180°﹣45°﹣60°=75°,∠FNC=15°,
∵sin∠FNC=![]() ,NC=x,
,NC=x,
∴FC=![]() x,
x,
∴NE=DF=![]()
∴点N到AD的距离为![]()
(3)∵sin∠NCF=![]() ,
,
∴FN=![]() x,
x,
∵P为DC的中点,
∴PD=CP=![]() ,
,
∴PF=![]() x+
x+![]() ,
,
∴△PMN的面积y=梯形MDFN的面积﹣△PMD的面积﹣△PNF的面积
=![]() (
(![]() x+
x+![]() ﹣x)(
﹣x)(![]() x+2
x+2![]() )﹣
)﹣![]() (
(![]() ﹣x)×
﹣x)×![]() ﹣
﹣![]() (
(![]() x+
x+![]() )(
)(![]() x)
x)
=![]()
即y是x的二次函数,
∵![]() <0,
<0,
∴y有最大值,
当x=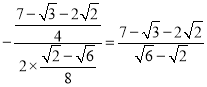 时,
时,
y有最大值为![]()


科目:初中数学 来源: 题型:
【题目】端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.
(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
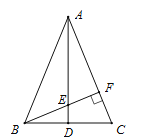
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°
求证:△AEF≌△BCF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为6cm,当OP=6cm时,点P在_________;当OP__________时,点P在圆内;当OP___________时,点P不在圆外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() . 给出下列结论:
. 给出下列结论:
①![]() 是方程组的解;②当k=
是方程组的解;②当k=![]() 时,x ,y的值互为相反数;
时,x ,y的值互为相反数;
③若方程组的解也是方程x + y =4 – k的解,则k=1;
④若![]() ,则
,则![]() . 其中正确的是________。
. 其中正确的是________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.请用含有b的式子表示a,并帮该物流公司设计租车方案;
(3)在(2)的条件下,若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com