
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�������������������Ŀ��A������B��ƹ����C������D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ͼ����ͼ��������ش��������⣺
��1����α������ѧ�����ж����ˣ�
��2�����㽫����ͳ��ͼ����������
��3������У����ѧ��1900�ˣ�������Ƹ�Уϲ��D��Ŀ��������
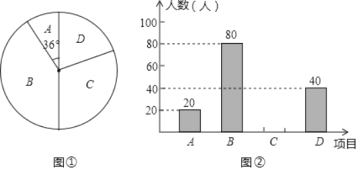
���𰸡�(1)200�ˣ���2��60�ˣ���ȫͼ�μ���������3��380��.
��������
(1)��ϲ���������������ϲ�������������ռ�İٷֱ�,���������Щ�������ѧ����;
(2)����������ȥϲ������ƹ��������������,�������ϲ�����������,�Ӷ���ȫͳ��ͼ;
(3)������������ϲ�������������ռ�İٷֱȿɵô�.
�⣺��1����������ã�20![]()
![]() =200���ˣ�
=200���ˣ�
����α������ѧ����200�ˣ�
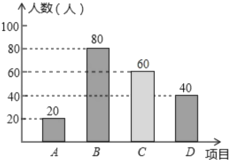
(2)ϲ�������������:200-20-80-40=60(��),��ȫͼ����ͼ��ʾ:
(3)1900![]()
![]() =380��
=380��
��:��Уϲ��D��Ŀ������ԼΪ380��.


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ��4���ֱ�д�����֩�2����1��0��1��2��С�����dz����ֲ�ͬ������ȫ����ͬ���ִӺ��������ȡ��һ��С����С���ϵ�����Ϊm����P������Ϊ��m��m2+1�������P����������y=��4x2+8x+5��x����Χ�ɵ������ڣ����߽磩�ĸ�����___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
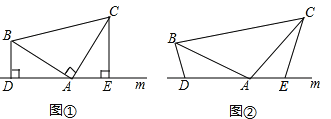
����Ŀ����1����ͼ�٣���֪���ڡ�ABC�У���BAC��90�㣬AB=AC��ֱ��m������A��BD��ֱ��m, CE��ֱ��m,����ֱ�Ϊ��D��E.֤��:DE=BD+CE.
��2����ͼ�ڣ�����1���е�������Ϊ���ڡ�ABC�У�AB=AC��D��A��E���㶼��ֱ��m��,�����С�BDA=��AEC=��BAC=��,���Ц�Ϊ����۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
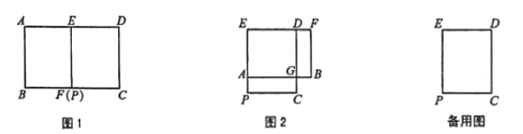
����Ŀ����֪��ͼ 1������ABC �У���ACB��90����BC��AC���� D �� AB �ϣ�DE��AB�� BC �� E���� F �� AE ���е�
��1�� д���߶� FD ���߶� FC �Ĺ�ϵ��֤����
��2�� ��ͼ 2������BDE �Ƶ� B ��ʱ����ת����0��������90�����������������䣬�߶� FD ���߶� FC �Ĺ�ϵ�Ƿ�仯��д����Ľ��۲�֤����
��3�� ����BDE �Ƶ� B ��ʱ����תһ�ܣ���� BC��4��BE��2![]() ��ֱ��д���߶� BF �ķ�Χ��
��ֱ��д���߶� BF �ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
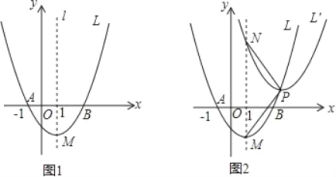
����Ŀ����ͼ1����֪������L��y=ax2+bx��1.5(a��0)��x�ύ�ڵ�A(-1,0)�͵�B������ΪM���Գ���Ϊֱ��l��x=1.
��1��ֱ��д����B�����꼰һԪ���η���ax2+bx��1.5=0�Ľ⣮
��2����������L�Ľ���ʽ������M�����꣮
��3����ͼ2�����P��������L�ϵ�һ�����㣬��������Lƽ�ƣ�ʹ����픵�������P���õ���������L����L����ֱ��l�ཻ�ڵ�N�����P�ĺ�����Ϊm
�ٵ�m=5ʱ��PM��PN��������������ϵ����˵�����ɣ�
�ڵ�mΪ����1������ʵ��ʱ�����еĹ�ϵʽ��������Ϊʲô��
���Ƿ���������ĵ�P��ʹ��PMNΪ�ȱ������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���˽���꼶ѧ������״�����Ӿ��꼶ѧ���������ȡ����ѧ���������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ��������ݲ��Գɼ����������������в�������ͳ��ͼ��
��1����γ������������������ ������ȫ����ͼ��
��2��D�ȼ�ѧ������ռ�����������İٷֱ�Ϊ ��������ͳ��ͼ��C�ȼ�����Ӧ��Բ�Ľ�Ϊ ����
��3����У���꼶ѧ����1500�ˣ������������A�ȼ���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԭ��O��ֱ��l1��˫����![]() ��һ������ΪA��1��m����
��һ������ΪA��1��m����
��1����ֱ��l1�ı���ʽ��
��2��������P��n��0����n��0���Ҵ�ֱ��x���ֱ����ֱ��l1��˫����![]() �Ľ���ֱ�ΪB��C������Bλ�ڵ�C�Ϸ�ʱ��ֱ��д��n��ȡֵ��Χ��
�Ľ���ֱ�ΪB��C������Bλ�ڵ�C�Ϸ�ʱ��ֱ��д��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
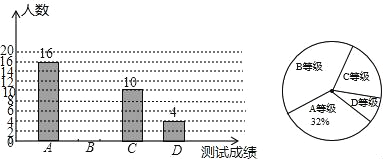
����Ŀ���������ڵ����㳡��������ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС����������㳡�����Ŀ�����������һ�γ������飬�Ѿ�������㳡�����Ŀ�����Ϊ�ĸ���Σ�A���dz���ͬ��B����ͬ��Ҫ��ʱ�����ƣ�C������ν��D������ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��

�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2����C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������ж����㳡�����Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��--------ͼ�α任�е���ѧ����
�����龳��
��ͼ1����֪����![]() �У���
����![]() ��
��![]() ���е㣬����
���е㣬����![]() ��������
��������![]() ��
��![]() �������õ��ı���
�������õ��ı���![]() ���ı���
���ı���![]() ��
��
��1����֤���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
����̽����
���־���![]() λ�ò��䣬������
λ�ò��䣬������![]() ��ͼ1��λ�ÿ�ʼ���Ƶ�
��ͼ1��λ�ÿ�ʼ���Ƶ�![]() ����ʱ�뷽����ת������ת��Ϊ
����ʱ�뷽����ת������ת��Ϊ![]() ��
��![]() ���������У�������������⣬������
���������У�������������⣬������
��2����ͼ2��������![]() ��ת����
��ת����![]() �����߶�
�����߶�![]() ��ʱ���߶�
��ʱ���߶�![]() ǡ�þ�����
ǡ�þ�����![]() ����
����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .�ж��ı���
.�ж��ı���![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3�����![]() ��������ѡһ��������ѡ���⣮
��������ѡһ��������ѡ���⣮
A���ھ���![]() ��ת�����У������߶�
��ת�����У������߶�![]() ��
��![]() ����
����![]() ʱ��ֱ��д����ת��
ʱ��ֱ��д����ת��![]() �Ķ�����
�Ķ�����
B����֪����![]() �У�
�У�![]() ���ھ���
���ھ���![]() ��ת�����У������߶�
��ת�����У������߶�![]() ��
��![]() ����
����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com