
【题目】综合与实践--------图形变换中的数学问题
问题情境:
如图1,已知矩形![]() 中,点
中,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .将矩形
.将矩形![]() 沿
沿![]() 剪开,得到四边形
剪开,得到四边形![]() 和四边形
和四边形![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
操作探究:
保持矩形![]() 位置不变,将矩形
位置不变,将矩形![]() 从图1的位置开始,绕点
从图1的位置开始,绕点![]() 按逆时针方向旋转,设旋转角为
按逆时针方向旋转,设旋转角为![]() (
(![]() ).操作中,提出了如下向题,请你解答:
).操作中,提出了如下向题,请你解答:
(2)如图2,当矩形![]() 旋转到点
旋转到点![]() 落在线段
落在线段![]() 上时,线段
上时,线段![]() 恰好经过点
恰好经过点![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() .判断四边形
.判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)请从![]() 两题中任选一题作答,我选择题.
两题中任选一题作答,我选择题.
A.在矩形![]() 旋转过程中,连接线段
旋转过程中,连接线段![]() 和
和![]() .当
.当![]() 时,直接写出旋转角
时,直接写出旋转角![]() 的度数.
的度数.
B.已知矩形![]() 中,
中,![]() .在矩形
.在矩形![]() 旋转过程中,连接线段
旋转过程中,连接线段![]() 和
和![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
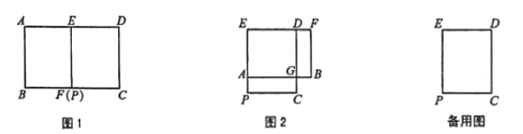
【答案】(1)见解析;(2)见解析;(3)A:60°或300°,B:![]() 或
或![]()
【解析】
(1)由![]() 矩形ABCD的边
矩形ABCD的边![]() 的中点可得ED//FC,ED=FC,根据有一个角是直角的平行四边形是矩形进行解答即可;(2)由(1)可得四边形EPCD为矩形,根据EA=ED即可证明四边形EPCD为正方形;(3)A题①当旋转到如图位置时,连接PF,由AP=BP可得∠PAB=∠PBA,即可证明∠PAE=∠PBF,进而利用SAS可证明△PAE≌△PBF,可得PE=PF,由PE=EF即可证明三角形PEF是等边三角形,可得旋转角∠PEF=60°,②当旋转到如图位置时,连接PF,同①可得∠PEF=60°,可得旋转角为300°;B题:在A题的基础上,①过P作PH⊥EA延长线于H,可得∠HEP=30°,根据∠HEP的三角函数可得HP、HE的长,进而可得AH的长,进而利用勾股定理求出AP的长即可,②过A作AH垂直PE延长线于H,可得∠AEH=30°,根据∠AEH的三角函数可求出AH、HE的长,进而可得PH的长,利用勾股定理求出AP的长即可.
的中点可得ED//FC,ED=FC,根据有一个角是直角的平行四边形是矩形进行解答即可;(2)由(1)可得四边形EPCD为矩形,根据EA=ED即可证明四边形EPCD为正方形;(3)A题①当旋转到如图位置时,连接PF,由AP=BP可得∠PAB=∠PBA,即可证明∠PAE=∠PBF,进而利用SAS可证明△PAE≌△PBF,可得PE=PF,由PE=EF即可证明三角形PEF是等边三角形,可得旋转角∠PEF=60°,②当旋转到如图位置时,连接PF,同①可得∠PEF=60°,可得旋转角为300°;B题:在A题的基础上,①过P作PH⊥EA延长线于H,可得∠HEP=30°,根据∠HEP的三角函数可得HP、HE的长,进而可得AH的长,进而利用勾股定理求出AP的长即可,②过A作AH垂直PE延长线于H,可得∠AEH=30°,根据∠AEH的三角函数可求出AH、HE的长,进而可得PH的长,利用勾股定理求出AP的长即可.
(1)∵四边形ABCD为矩形,
∴AD//BC,AD=BC,∠D=90°,
又∵点E、F是AD、BC的中点,
∴ED//FC,ED=FC,
∴四边形EPCD为平行四边形,
又∵∠D=90°,
∴平行四边形EPCD为矩形.
(2)四边形EAGD是正方形,理由如下:
由(1)得四边形EPCD为矩形,同理可得四边形ABFE为矩形
∴∠E=∠EAB=∠EDG=90°
∴四边形EAGD是矩形
又∵EA=ED
∴矩形EAGD是正方形.
(3)A题:①当旋转到如图位置时,∠PEF为旋转角,连接PF,
∵AP=BP,
∴∠PAB=∠PBA,
∵∠EAB=∠ABF=90°,
∴∠PAE=∠PBF,
∵AE=BF,∠PAE=∠PBF,AP=BP,
∴△PAE≌△PBF,
∴PE=PF,
∵PE=EF,
∴PE=PF=EF,
∴三角形PEF是等边三角形,
∴∠PEF=60°,即旋转角为60°,
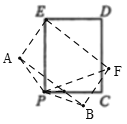
②当旋转到如图位置时,连接PF,
∵AP=BP,
∴∠PAB=∠PBA,
∴∠PAE=∠PBF,
∵AE=BF,∠PAE=∠PBF,PA=PB,
∴△PAE≌△PBF,
∴PF=PE,
∵PE=EF,
∴PE=PF=EF,
∴△PEF是等边三角形,
∴∠PEF=60°,
∴旋转角为360°-60°=300°.

综上所述:旋转角为60°或300°.
B题:①如图,过P作PH⊥EA延长线于H,
由A①得∠PEF=60°,
∵∠AEF=90°,
∴∠HEP=30°,
∴HP=![]() PE=
PE=![]() ×10=5,HE=PE
×10=5,HE=PE![]() cos30°=5
cos30°=5![]() ,
,
∴AH=HE-AE=5![]() -4
-4![]() =
=![]() ,
,
∴AP=![]() =
=![]() =2
=2![]() ,
,

②如图,过A作AH垂直PE延长线于H,
由A②得∠PEF=60°,
∵∠AEF=90°,
∴∠AEH=30°,
∴AH=![]() AE=2
AE=2![]() ,HE=AE
,HE=AE![]() cos30°=6,
cos30°=6,
∴PH=PE+HE=10+6=16,
∴AP=![]() =
=![]() =2
=2![]() .
.

综上所述:AP的长为2![]() 或2
或2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
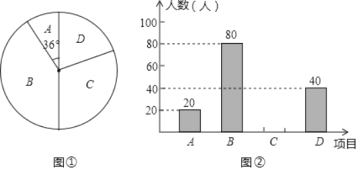
【题目】某学校为了增强学生体质,决定开放以下球类活动项目:A.篮球、B.乒乓球、C.排球、D.足球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图①,图②),请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图补充完整;
(3)若该校共有学生1900人,请你估计该校喜欢D项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读理解:
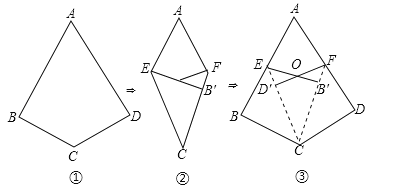
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=120°时,∠AEB′= °;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
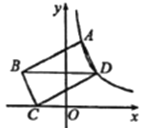
【题目】如图,在平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在
在![]() 轴上,对角线
轴上,对角线![]() 轴,若
轴,若![]() 两点的横坐标分别为1,2,
两点的横坐标分别为1,2,![]() 的长为
的长为![]() ,则
,则![]() 的值为____.
的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.
![]() 如果从袋中任意摸出一个球是红球的概率为
如果从袋中任意摸出一个球是红球的概率为![]() ,那么袋中有黄球多少个?
,那么袋中有黄球多少个?
![]() 在
在![]() 的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:

(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 台州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:p=![]() t+16,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
t+16,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com