
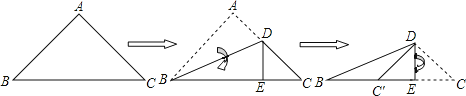
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC′平分∠BDE;②BC长为![]() +1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
+1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
【答案】③④
【解析】分析:根据等腰直角三角形的性质得到AB=AC=![]() BC,∠ABC=∠C=45°,由于Rt△ABD折叠得到Rt△EBD,根据折叠的性质得∠DBE=
BC,∠ABC=∠C=45°,由于Rt△ABD折叠得到Rt△EBD,根据折叠的性质得∠DBE=![]() ∠ABC=22.5°,DE=AD=a,∠DEB=90°,易得∠CDE=45°,DC=
∠ABC=22.5°,DE=AD=a,∠DEB=90°,易得∠CDE=45°,DC=![]() a;又由于Rt△DC′E由Rt△DCE折叠得到,则∠C′DE=∠CDE=45°,∠DC′E=45°,可计算出∠BDC′=∠DC′E﹣∠DBE=22.5°,于是可判断DC′不平分∠BDE;易得AC=AD+DC=a+
a;又由于Rt△DC′E由Rt△DCE折叠得到,则∠C′DE=∠CDE=45°,∠DC′E=45°,可计算出∠BDC′=∠DC′E﹣∠DBE=22.5°,于是可判断DC′不平分∠BDE;易得AC=AD+DC=a+![]() a,利用BC=
a,利用BC=![]() AC可得到BC长为(
AC可得到BC长为(![]() +2)a;由∠DBC=∠BDC′=22.5°可得到△B C′D是等腰三角形;计算△CED的周长为DE+EC+DC=a+a+
+2)a;由∠DBC=∠BDC′=22.5°可得到△B C′D是等腰三角形;计算△CED的周长为DE+EC+DC=a+a+![]() a=(
a=(![]() +2)a,则有△CED的周长等于BC的长.
+2)a,则有△CED的周长等于BC的长.
详解:∵△ABC为等腰直角三角形,∴AB=AC=![]() BC,∠ABC=∠C=45°.∵Rt△ABD折叠得到Rt△EBD,∴∠DBE=
BC,∠ABC=∠C=45°.∵Rt△ABD折叠得到Rt△EBD,∴∠DBE=![]() ∠ABC=22.5°,DE=AD=a,∠DEB=90°,∴△DCE为等腰直角三角形,∴∠CDE=45°,DC=
∠ABC=22.5°,DE=AD=a,∠DEB=90°,∴△DCE为等腰直角三角形,∴∠CDE=45°,DC=![]() a.∵Rt△DC′E由Rt△DCE折叠得到,∴∠C′DE=∠CDE=45°,∠DC′E=45°,∴∠BDC′=∠DC′E﹣∠DBE=22.5°,∴DC′不平分∠BDE,所以①错误;
a.∵Rt△DC′E由Rt△DCE折叠得到,∴∠C′DE=∠CDE=45°,∠DC′E=45°,∴∠BDC′=∠DC′E﹣∠DBE=22.5°,∴DC′不平分∠BDE,所以①错误;
∵AC=AD+DC=a+![]() a,∴BC=
a,∴BC=![]() AC=
AC=![]() (a+
(a+![]() a)=(
a)=(![]() +2)a,所以②错误;
+2)a,所以②错误;
∵∠DBC=∠BDC′=22.5°,∴△B C′D是等腰三角形,所以③正确;
∵△CED的周长=DE+EC+DC=a+a+![]() a=(
a=(![]() +2)a,∴△CED的周长等于BC的长,所以④正确.
+2)a,∴△CED的周长等于BC的长,所以④正确.
故答案为:③④.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣![]() <0的解集.(直接写出答案)
<0的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处(如图1).
(1)如图2,设折痕与边BC交于点O,连接,OP、OA.已知△OCP与△PDA的面积比为1:4,求边AB的长;
(2)动点M在线段AP上(不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN、CA,交于点F,过点M作ME⊥BP于点E.
①在图1中画出图形;
②在△OCP与△PDA的面积比为1:4不变的情况下,试问动点M、N在移动的过程中,线段EF的长度是否发生变化?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛.从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,已知A组的频数a比B组的频数b小24,绘制统计频数分布直方图(未完成)和扇形图如下,请解答下列问题:
(1)样本容量为:______,a为______;
(2)n为________,E组所占比例为________;
(3)补全频数分布直方图;
(4)若成绩在80分以上记作优秀,全校共有2000名学生,估计成绩优秀学生有_________名.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与双曲线 ![]() (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE , 则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE , 则b= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( ![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)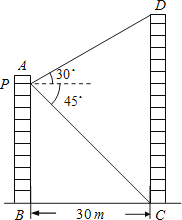
查看答案和解析>>
科目:初中数学 来源: 题型:
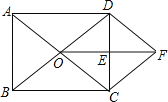
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com