
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( ![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)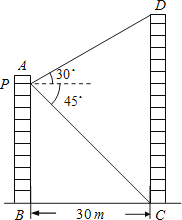
【答案】解:过点P作PE⊥CD于E,则四边形BCEP是矩形.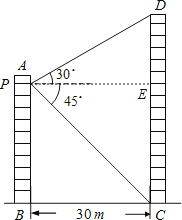
∴PE=BC=30.
在Rt△PDE中,∵∠DPE=30°,PE=30,
∴DE=PE×tan30°=30× ![]() =10
=10 ![]() .
.
在Rt△PEC中,∵∠EPC=45°,PE=30,
∴CE=PE×tan45°=30×1=30.
∴CD=DE﹢CE=30﹢10 ![]() =30﹢17.3≈47(m)
=30﹢17.3≈47(m)
答:建筑物CD的高约为47 m.
【解析】过点P作PE⊥CD于E,则四边形BCEP是矩形,得到PE=BC=30,在Rt△PDE中,利用∠DPE=30°,PE=30,求得DE的长;在Rt△PEC中,利用∠EPC=45°,PE=30求得CE的长,利用CD=DE﹢CE即可求得结果.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.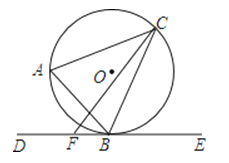
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则①DC′平分∠BDE;②BC长为![]() +1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
+1)a;③△BC′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确的序号是_______.
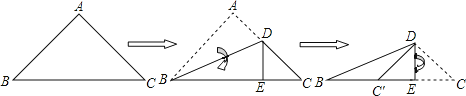
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )

A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:

(1)本次调查的样本容量为________.
(2)在表中,m=_______,n=_________.
(3)补全频数颁分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c经过点A(﹣3,0)、B(0,3)、C(1,0)三点.
(1)求抛物线的解析式和顶点D的坐标;
(2)如图1,将抛物线的对称轴绕抛物线的顶点D顺时针旋转60°,与直线y=﹣x交于点N.在直线DN上是否存在点M,使∠MON=75°.若存在,求出点M的坐标;若不存在,请说明理由;
(3)点P、Q分别是抛物线y=ax2+bx+c和直线y=﹣x上的点,当四边形OBPQ是直角梯形时,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年上半年某市各级各类中小学(含中等职业学校)开展了“万师访万家”活动.某县家访方式有:A.上门走访;B.电话访问;C.网络访问(班级微信或QQ群);D.其他.该县教育局负责人从“万师访万家”平台上随机抽取本县一部分老师的家访情况,绘制了如图所示两幅尚不完整的统计图.
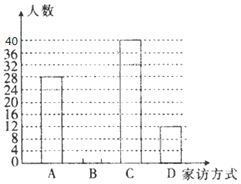
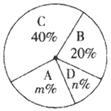
根据图中提供的信息,解答下列问题:
(1)本次抽样调查的样本是________________________________,样本容量为________,
扇形统计图中,“A”所对应的圆心角的度数为多少?
(2)请补全条形统计图.
(3)已知该县共有3500位老师参与了这次“万师访万家”活动,请估计该县共有多少位老师采用的是上门走访的方式进行家访的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.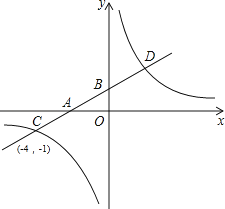
(1)求反比例函数与一次函数的解析式;
(2)若点P为坐标轴上一点,且S△ACP=2S△ABO , 请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com