
【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.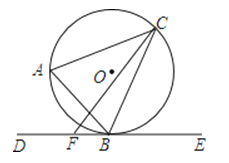
【答案】证明:(1)如图,连接BO并延长交⊙O于点M,连接MC,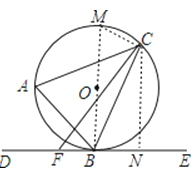
∴∠A=∠M,∠MCB=90°,
∴∠M+∠MBC=90°,
∵DE是⊙O的切线,
∴∠CBE+∠MBC=90°,
∴∠CBE=∠M,
∴∠CBE=∠A;
(2)解:过点C作CN⊥DE于点N,
∴∠CNF=90°,
由(1)得,∠M=∠CBE=∠A,
∴tanM=tan∠CBE=tanA=2,
在Rt△BCM中,
∵BM=5,tanM=2,
∴![]() ,
,
在Rt△CNB中,
∵![]() ,
,![]() ,
,
∴CN=4,BN=2,
∵BF=2,
∴FN=BF+BN=4,
在Rt△FNC中,
∵FN=4,CN=4,
∴![]() .
.
【解析】(1)连接BO并延长交⊙O于点M,连接MC,根据圆周角定理求出∠A=∠M,∠MCB=90°,求出∠M+∠MBC=90°,根据切线性质求出∠CBE+∠MBC=90°,推出∠CBE=∠M即可;
(2)过点C作CN⊥DE于点N,求出∠CNF=90°,求出tanM=tan∠CBE=tanA=2,解直角三角形求出BC、CN、BN,求出FN,根据勾股定理求出即可.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
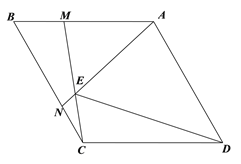
【题目】如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
(1)证明△BCM≌△CAN;
(2)∠AEM= °;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
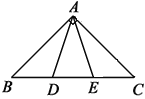
【题目】如图,在△ABC中, ∠BAC=90°, AB=AC=2![]() ,点D,E均在边BC上,且∠DAE=45°,若BD=1,则DE=__________.
,点D,E均在边BC上,且∠DAE=45°,若BD=1,则DE=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
(1)求y与x之间的函数关系式?(不要求写自变量的取值范围);
(2)求矩形ABCD的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=110°,∠B=85°将△BMN沿着MN翻折,得到△FMN,若MF∥AD,FN∥DC,则∠C的度数为( )
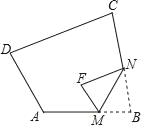
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣![]() <0的解集.(直接写出答案)
<0的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个建筑物AB和CD的水平距离为30m,张明同学住在建筑物AB内10楼P室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.( ![]() 取1.73,结果保留整数.)
取1.73,结果保留整数.)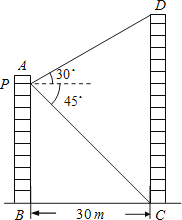
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com