
【题目】如图,在四边形ABCD中,∠A=110°,∠B=85°将△BMN沿着MN翻折,得到△FMN,若MF∥AD,FN∥DC,则∠C的度数为( )
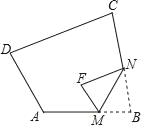
A. 70° B. 80° C. 90° D. 100°
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
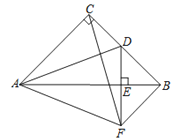
【题目】如图,在![]() 中,∠ACB=90°,AC=BC=4,D为BC的中点,
中,∠ACB=90°,AC=BC=4,D为BC的中点, ![]() ,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
,垂足为E.过点B作BF//AC交DE的延长线于点F,连接CF,AF.现有如下结论:
①BF=2;②![]() ;③AD平分∠CAB;④AF=
;③AD平分∠CAB;④AF=![]() ;⑤∠CAF=∠CFB.其中正确的结论是( )
;⑤∠CAF=∠CFB.其中正确的结论是( )
A. ①②③ B. ①②④ C. ②③④⑤ D. ①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数![]() 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
(1)如图,若tanB=2,则![]() 的值为
的值为
(2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若![]() , 则tanB的值为
, 则tanB的值为 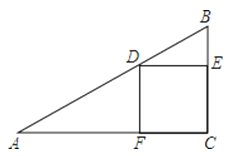
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
(1)求证:∠CBE=∠A;
(2)若⊙O的直径为5,BF=2,tanA=2,求CF的长.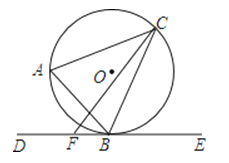
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=45°,点P、Q分别是边OA,OB上的两点,将∠O沿PQ折叠,点O落在平面内点C处.若折叠后PC⊥QB,则∠OPQ的度数是____________.
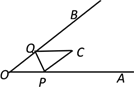
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C的度数等于( )
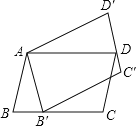
A. 100° B. 105° C. 115° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:

(1)本次调查的样本容量为________.
(2)在表中,m=_______,n=_________.
(3)补全频数颁分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com