
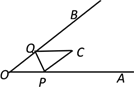
【题目】如图,已知∠AOB=45°,点P、Q分别是边OA,OB上的两点,将∠O沿PQ折叠,点O落在平面内点C处.若折叠后PC⊥QB,则∠OPQ的度数是____________.
【答案】22.5°或112.5°
【解析】分析:根据题意画出符合要求的图形,如下图1和图2,分点C在OA下方和OB上方两种情况结合折叠的性质及已知条件解答即可.
详解:
(1)如图1,当点C在OA的下方时,延长CP交OB于点D,
∵CP⊥OB,
∴∠ODC=90°,
∵∠AOB=45°,
∴∠DPC=45°,
∴∠OPQ+∠CPQ=45°+180°=225°,
∵由折叠的性质可知∠OPQ=∠CPQ,
∴∠OPQ=112.5°;
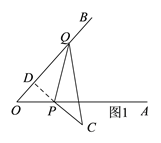
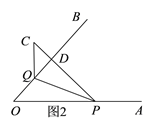
(2)如图2,当点C在OB的上方时,
∵PC⊥OB,
∴∠ODP=90°,
又∵∠AOB=45°,
∴∠OPQ+∠CPQ=∠OPC=45°,
∵由折叠的性质可知∠OPQ=∠CPQ,
∴∠OPQ=22.5°.
综上所述,当PC⊥OB时,∠OPQ的度数为112.5°或22.5°.
故答案为:112.5°或22.5°.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:
①旋转角是____度;
②线段OD的长为_____;
③求∠BDC的度数.
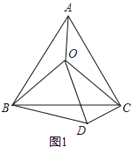
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,∠A0B=135,OA=1,0B=2,求0C的长.
小明同学借用了图1的方法,将△BAO绕点B顺时针旋转后得到△BCD,请你继续用小明的思路解答,或是选择自己的方法求解.

查看答案和解析>>
科目:初中数学 来源: 题型:
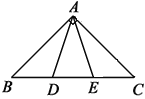
【题目】如图,在△ABC中, ∠BAC=90°, AB=AC=2![]() ,点D,E均在边BC上,且∠DAE=45°,若BD=1,则DE=__________.
,点D,E均在边BC上,且∠DAE=45°,若BD=1,则DE=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=110°,∠B=85°将△BMN沿着MN翻折,得到△FMN,若MF∥AD,FN∥DC,则∠C的度数为( )
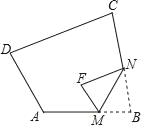
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(1)计算AC2+BC2的值等于 ;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个平行四边形ABEF,使得该平行四边形的面积等于16;
(3)请在如图所示的网格中,用无刻度的直尺,画出一个矩形ABMN,使得该矩形的面积等于AC2+BC2.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(n,﹣2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b﹣![]() <0的解集.(直接写出答案)
<0的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛.从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,已知A组的频数a比B组的频数b小24,绘制统计频数分布直方图(未完成)和扇形图如下,请解答下列问题:
(1)样本容量为:______,a为______;
(2)n为________,E组所占比例为________;
(3)补全频数分布直方图;
(4)若成绩在80分以上记作优秀,全校共有2000名学生,估计成绩优秀学生有_________名.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com